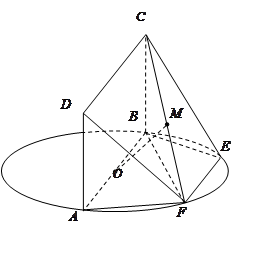已知中心在原点,焦点在 轴上的椭圆
轴上的椭圆 的离心率为
的离心率为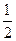 ,且经过点
,且经过点 ,过点
,过点 的直线
的直线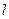 与椭圆
与椭圆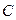 相交于不同的两点
相交于不同的两点 .
.
(Ⅰ)求椭圆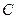 的方程;
的方程;
(Ⅱ)是否存直线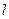 ,满足
,满足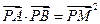 ?若存在,求出直线
?若存在,求出直线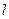 的方程;若不存在,请说明理由
的方程;若不存在,请说明理由
.(本小题满分13分)设 ,其中
,其中 为正实数.
为正实数.
(1)当 时,求
时,求 的极值点;
的极值点;
(2)若 为
为 上的单调函数,求
上的单调函数,求 的取值范围.
的取值范围.
.(本小题满分13分)如图,渔船甲位于岛屿 的南偏西
的南偏西 方向的
方向的 处,且与岛屿
处,且与岛屿 相距12海里,渔船乙以10海里/小时的速度从岛屿
相距12海里,渔船乙以10海里/小时的速度从岛屿 出发沿正北方向航行,若渔船甲同时从
出发沿正北方向航行,若渔船甲同时从 处出发沿北偏东
处出发沿北偏东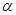 的方向追赶渔船乙,刚好用2小时追上.
的方向追赶渔船乙,刚好用2小时追上.
(1)求渔船甲的速度;
(2)求 的值.
的值.
已知函数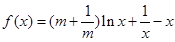 ,(其中常数
,(其中常数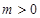 )
)
(1)当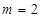 时,求
时,求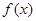 的极大值;
的极大值;
(2)试讨论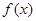 在区间
在区间 上的单调性;
上的单调性;
(3)当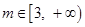 时,曲线
时,曲线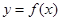 上总存在相异两点
上总存在相异两点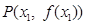 、
、 ,使得曲线
,使得曲线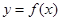 在点
在点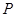 、
、 处的切线互相平行,求
处的切线互相平行,求 的取值范围.
的取值范围.
.(本题满分12分)已知椭圆 的离心率为
的离心率为 ,短轴的一个端点到右焦点的距离为2,
,短轴的一个端点到右焦点的距离为2,
(1)试求椭圆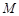 的方程;
的方程;
(2)若斜率为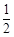 的直线
的直线 与椭圆
与椭圆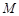 交于
交于 、
、 两点,点
两点,点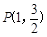 为椭圆
为椭圆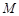 上一点,记直线
上一点,记直线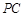 的斜率为
的斜率为 ,直线
,直线 的斜率为
的斜率为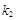 ,试问:
,试问: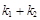 是否为定值?请证明你的结论.
是否为定值?请证明你的结论.
.(本题满分12分)如图,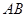 为圆
为圆 的直径,点
的直径,点 、
、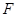 在圆
在圆 上,
上, ,矩形
,矩形 的边
的边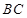 垂直于圆
垂直于圆 所在的平面,且
所在的平面,且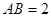 ,
,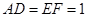 .
.
(1)求证: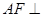 平面
平面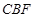 ;
;
(2)设 的中点为
的中点为 ,求证:
,求证: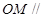 平面
平面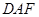 ;
;
(3)求三棱锥的体积 .
.