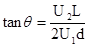如图所示，在xoy平面内，MN和x轴之间有平行于y轴的匀强电场和垂直于xoy平面的匀强磁场，y轴上离坐标原点3L的A点处有一电子枪，可以沿+x方向射出速度为v0的电子（质量为m，电量为e）。如果电场和磁场同时存在，电子将做匀速直线运动.如果撤去磁场只保留电场，电子将从P点离开电场，P点的坐标是（2L,5L）.不计重力的影响，求：
（1）电场强度E和磁感应强度B的大小及方向；
（2）如果撤去电场，只保留磁场，电子将从x轴上的D点（图中未标出）离开磁场，求D点的坐标及电子在磁场中运动的时间.
在一个标准大气压下，1kg冰在0℃时吸收336kJ的热量后变成同温度的水，外界同时对系统做了11kJ的功，阿伏伽德罗常数NA=6.0×1023mol-1，水的摩尔质量
M=18g•mol-1.问
(Ⅰ)此过程中系统的内能变化了多少？
(Ⅱ)1kg冰所含的分子数为多少？(结果保留2位有效数字)
(18分)
如图甲,电阻不计的轨道MON与PRQ平行放置，ON及RQ与水平面的倾角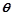
=53°，MO及PR部分的匀强磁场竖直向下，ON及RQ部分的磁场平行轨道向下，磁场的磁感应强度大小相同，两根相同的导体棒ab和cd分别放置在导轨上，与导轨垂直并始终接触良好。棒的质量m=1.0kg，R=1.0
，长度与导轨间距相同，L=1.0m，棒与导轨间动摩擦因数
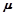=0.5，现对ab棒施加一个方向向右，大力随乙图规律变化的力F的作用，同时由静止释放cd棒，则ab棒做初速度为零的匀加速直线运动，g取10m/s2，求
(1)ab棒的加速度大小；
(2)磁感应强度B的大小；
(3)若已知在前2s内外力做功W=30J，求这一过程中电路产生的焦耳热；
(4)求cd棒达到最大速度所需的时间.
如图所示，一小球自平台上水平抛出，恰好落在临近平台的一倾角为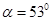
的光滑斜面顶端，并刚好沿光滑斜面下滑，已知斜面顶端与平台的高度差
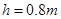，重力加速度
，
，
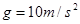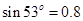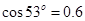，求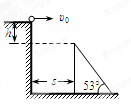
（1）小球水平抛出的初速度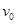
是多少？
（2）斜面顶端与平台边缘的水平距离s是多少？
（3）若斜面顶端高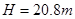
,则小球离开平台后经过多长时间t到达斜面底端？
如图所示，在水平向右的、强度E = 2000V/m的匀强电场中，质量m = 1.73毫克的带电粒子以大小v0 = 10m/s、方向和水平方向成30°的初速度从A点射入，发现它恰能做直线运动。以A点所在的等势面为参考平面，电场区域足够大，试求：
（1）粒子的电性和电量；
（2）粒子沿直线前进的最大距离；
（3）粒子可以获得的最大电势能。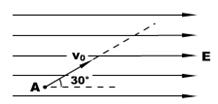
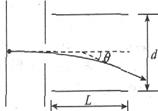
如图所示，一束初速度为零的带电粒子流经电压U1的加速电场加速后，沿垂直于偏转电场的场强方向进入偏转电场.已知偏转电场两平行板间的电势差为U2，极板长为L，两板间的距离为d，带电粒子通过偏转电场时的偏转角为θ.试证明:
