如图,O是正方形ABCD的中心,PO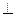 底面ABCD,E是PC的中点.求证:
底面ABCD,E是PC的中点.求证:
(Ⅰ)PA∥平面BDE;
(Ⅱ)平面PAC 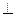 平面BDE
平面BDE
利用余弦函数y=cosx的图像,比较x=0,x=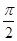 附近的平均变化率的大小。
附近的平均变化率的大小。

一书店预计一年内要销售某种书15万册,欲分几次订货,如果每次订货要付手续费30元,每千册书存放一年要耗库费40元,并假设该书均匀投放市场,问此书店分几次进货、每次进多少册,可使所付的手续费与库存费之和最少?
某工厂生产某种产品,已知该产品的月生产量 (吨)与每吨产品的价格
(吨)与每吨产品的价格 (元/吨)之间的关系式为:
(元/吨)之间的关系式为: ,且生产x吨的成本为
,且生产x吨的成本为 (元).问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入─成本)
(元).问该厂每月生产多少吨产品才能使利润达到最大?最大利润是多少?(利润=收入─成本)
当室内的有毒细菌开始增加时,就要使用杀菌剂.刚开始使用的时候,细菌数量还会继续增加,随着时间的增加,它增加幅度逐渐变小,到一定时间,细菌数量开始减少.如果使用杀菌剂t小时后的细菌数量为b(t)=105+104t-103t2.
(1)求细菌在t=5与t=10时的瞬时速度;(2)细菌在哪段时间增加,在哪段时间减少?为什么?