(本小题满分12分)
从集合 中,抽取三个不同元素构成子集
中,抽取三个不同元素构成子集 .
.
(Ⅰ)求对任意的 (
( ),满足
),满足 的概率;
的概率;
(Ⅱ)若 成等差数列,设其公差为
成等差数列,设其公差为 ,求随机变量
,求随机变量 的分布列与数学期望。
的分布列与数学期望。
已知函数 .
.
(Ⅰ)求 在区间
在区间 上的最大值;
上的最大值;
(Ⅱ)若过点 存在
存在 条直线与曲线
条直线与曲线 相切,求
相切,求 的取值范围.
的取值范围.
设命题 :函数
:函数 的定义域为
的定义域为 ;命题
;命题 :不等式
:不等式 对一切
对一切 均成立。
均成立。
(Ⅰ)如果 是真命题,求实数
是真命题,求实数 的取值范围;
的取值范围;
(Ⅱ)如果命题“ 或
或 ”为真命题,且“
”为真命题,且“ 且
且 ”为假命题,求实数
”为假命题,求实数 的取值范围.
的取值范围.
(本小题满分14分) 已知函数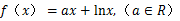
(Ⅰ)若a=2,求曲线y=f(x)在点x=1处的切线方程;
(Ⅱ)求f(x)的单调区间;
(Ⅲ)设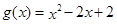 ,若对任意
,若对任意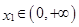 ,总存在
,总存在 ,使得
,使得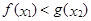 ,求a的取值范围.
,求a的取值范围.
(本小题满分13分)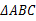 两个顶点A、B的坐标分别是
两个顶点A、B的坐标分别是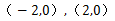 ,边AC、BC所在直线的斜率之积等于
,边AC、BC所在直线的斜率之积等于
(1)求顶点C的轨迹方程;
(2)求上述轨迹中以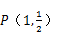 为中点的弦所在的直线方程.
为中点的弦所在的直线方程.
(本小题满分12分)已知四棱锥P-ABCD中,底面ABCD为菱形,且平面PAC垂直于底面ABCD,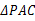 中,
中,
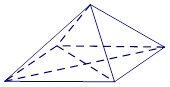
(Ⅰ)求证:平面PBD 平面PAC
平面PAC
(Ⅱ)若BD=PA=2,求四棱锥P-ABCD的体积