如图,圆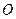 与
与 轴的正半轴的交点为
轴的正半轴的交点为 ,点
,点 、
、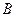 在圆
在圆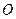 上,且点
上,且点 位于第一象限,点
位于第一象限,点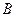 的坐标为
的坐标为
 ,
, .
.
(Ⅰ)求圆 的半径及
的半径及 点的坐标(用
点的坐标(用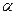 表示);
表示);
(Ⅱ)若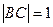 ,求
,求 的值.
的值.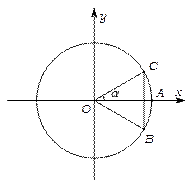
(本小题满分13分)如图,三棱柱 中,
中,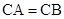 ,
, ,
, .
.
(1)证明: ;
;
(2)若 ,
, ,求二面角
,求二面角 的余弦值.
的余弦值.
(本小题满分13分)某教育主管部门到一所中学检查学生的体质健康情况.从全体学生中,随机抽取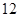 名进行体制健康测试,测试成绩(百分制)以茎叶图形式表示如下:
名进行体制健康测试,测试成绩(百分制)以茎叶图形式表示如下: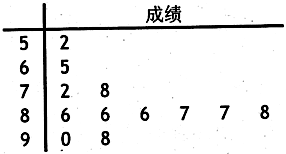
根据学生体制健康标准,成绩不低于 的为优良.
的为优良.
(1)将频率视为概率,根据样本估计总体的思想,在该校学生中任选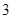 人进行体制健康测试,求至少有
人进行体制健康测试,求至少有 人成绩是“优良”的概率;
人成绩是“优良”的概率;
(2)从抽取的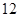 人中随机选取
人中随机选取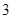 人,记
人,记 表示成绩“优良”的学生人数,求
表示成绩“优良”的学生人数,求 的分布列及期望.
的分布列及期望.
(本小题满分12分)已知函数 ,
, .
.
(1)求 的值;
的值;
(2)若 ,
, ,求
,求 的值.
的值.
(本题满分 12 分)本题共有 3 个小题,第 1 小题满分 3分,第 2 小题满分 4分,第 3小题满分5 分.
设数列 的首项
的首项 为常数,且
为常数,且 .
.
(1)证明: 是等比数列;
是等比数列;
(2)若 ,
, 中是否存在连续三项成等差数列?若存在,写出这三项,若不存在说明理由.
中是否存在连续三项成等差数列?若存在,写出这三项,若不存在说明理由.
(3)若 是递增数列,求
是递增数列,求 的取值范围.
的取值范围.
(本题满分 10 分)本题共有 2 个小题,第 1 小题满分 4 分,第 2 小题满分6分.
在平面直角坐标系 中,点
中,点 到两点
到两点 、
、 的距离之和等于4.设点
的距离之和等于4.设点 的轨迹为
的轨迹为 .
.
(1)写出轨迹 的方程;
的方程;
(2)设直线 与
与 交于
交于 、
、 两点,问
两点,问 为何值时
为何值时 此时|
此时| |的值是多少?
|的值是多少?