如图所示,质量为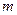 的物体在恒力
的物体在恒力 的作用下,沿着竖直平整的墙壁向下做匀速直线运动,已知恒力
的作用下,沿着竖直平整的墙壁向下做匀速直线运动,已知恒力 与竖直方向的夹角为
与竖直方向的夹角为 ,试求物体与墙壁间的动摩擦因数
,试求物体与墙壁间的动摩擦因数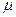 。
。
水平直线MN上方有垂直纸面向外的足够大的有界匀强磁场区域,磁感应强度为B,正、负电子同时从MN边界O点以与MN成300角的相同速度v射入该磁场区域(电子质量为m,电量为e) 经一段时间后从边界MN射出。求:
(1)它们从磁场中射出时,出射点间的距离;(画出电子运动的轨迹图)
(2)它们从磁场中射出的时间差。
2010年10月1日,我国成功发射了“嫦娥二号”探月卫星.“嫦娥二号”在距月球表面100 km高度的轨道上做圆周运动,这比“嫦娥一号”距月球表面200 km的圆形轨道更有利于对月球表面做出精细测绘.已知月球半径为1600km.求:“嫦娥一号”与“嫦娥二号”在各自圆轨道上运行速度的大小之比.
滑板运动是一项非常刺激的水上运动,研究表明,在进行滑板运动时,水对滑板的作用力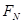 垂直于板面,大小为kv2,其中v为滑板速率(水可视为静止).某次运动中,在水平牵引力作用下,当滑板和水面的夹角
垂直于板面,大小为kv2,其中v为滑板速率(水可视为静止).某次运动中,在水平牵引力作用下,当滑板和水面的夹角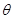 时(如图),滑板做匀速直线运动,相应的k是一个常数,人和滑板的总质量为
时(如图),滑板做匀速直线运动,相应的k是一个常数,人和滑板的总质量为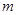 ,试求:(重力加速度为g,忽略空气阻力):
,试求:(重力加速度为g,忽略空气阻力):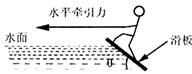
(1)水平牵引力的大小;
(2)滑板的速率;
一辆执勤的警车停在公路边,当警员发现从他旁边以10m/s的速度匀速行驶的货车严重超载时,决定前去追赶,经过6s后警车发动起来,并以2.5m/s2的加速度做匀加速运动,但警车的速度必须控制在90km/h以内。问:
(1)警车在追赶货车的过程中,两车之间的最大距离是多少?
(2)警车发动后至少经过多长时间才能追上货车?(保留3位有效数字)
如图所示,一个U形导体框架,其宽度L=1m,框架所在平面与水平面的夹用α=30°。其电阻可忽略不计。设匀强磁场与U形框架的平面垂直。匀强磁场的磁感强度B=0.2T。今有一条形导体ab,其质量为m=0.5kg,有效电阻R=0.1Ω,跨接在U形框架上,并且能无摩擦地滑动,求:
(1)由静止释放导体,导体ab下滑的最大速度vm;
(2)在最大速度vm时,在ab上释放的电功率。(g=10m/s2)。