（本小题满分12分）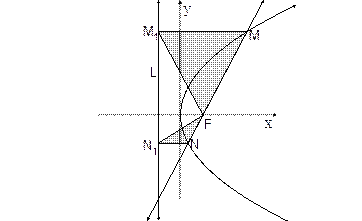
已知直线
过抛物线
的焦点
且与抛物线相交于两点
，自
向准线
作垂线，垂足分别为
．
(Ⅰ)求抛物线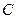
的方程；
(Ⅱ)证明：无论
取何实数时，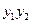
，
都是定值；
(III)记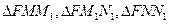
的面积分别为
，试判断
是否成立，并证明你的结论．
已知椭圆
的中心在原点，焦点在
轴上，离心率为
，它的一个顶点恰好是抛物线
的焦点．
（I）求椭圆的方程；
（II）直线
与椭圆交于
两点，
点位于第一象限，
是椭圆上位于直线两侧的动点．
（i）若直线
的斜率为
，求四边形
面积的最大值；
（ii）当点运动时，满足
，问直线的斜率是否为定值，请说明理由．
某理科考生参加自主招生面试，从7道题中（4道理科题3道文科题）不放回地依次任取3道作答．
（1）求该考生在第一次抽到理科题的条件下，第二次和第三次均抽到文科题的概率；
（2）规定理科考生需作答两道理科题和一道文科题，该考生答对理科题的概率均为
，答对文科题的概率均为
，若每题答对得10分，否则得零分．现该生已抽到三道题（两理一文），求其所得总分
的分布列与数学期望
．
已知平面内一动点
（
）到点
的距离与点
到
轴的距离的差等于1，
（1）求动点的轨迹
的方程；
（2）过点
的直线
与轨迹相交于不同于坐标原点
的两点
，求
面积的最小值．
已知函数
．
（1）当函数
在点
处的切线与直线
垂直时，求实数
的值；
（2）若
时，
恒成立，求实数的取值范围．
已知书架中甲层有英语书2本和数学书3本，乙层有英语书1本和数学书4本．现从甲、乙两层中各取两本书．
（1）求取出的4本书都是数学书的概率．
（2）求取出的4本书中恰好有1本是英语书的概率．