((本小题满分14分)
已知函数 .
.
(I)当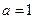 时,求函数
时,求函数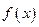 的单调区间;
的单调区间;
(II)若函数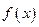 在区间
在区间 上无极值,求
上无极值,求 的取值范围;
的取值范围;
(III)已知 且
且 ,求证:
,求证: .
.
直线y=kx+b与曲线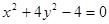 交于A、B两点,记△AOB的面积为S(O是坐标原点).
交于A、B两点,记△AOB的面积为S(O是坐标原点).
(1)求曲线的离心率;
(2)求在k=0,0<b<1的条件下,S的最大值;
(3)当|AB|=2,S=1时,求直线AB的方程.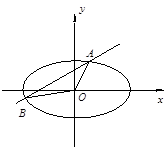
已知数列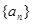 的各项均为正数,
的各项均为正数, 是数列
是数列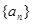 的前n项和,且
的前n项和,且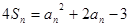 .
.
(1)求数列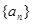 的通项公式;
的通项公式;
(2) 的值.
的值.
如图,多面体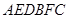 的直观图及三视图如图所示,
的直观图及三视图如图所示, 分别为
分别为 的中点.
的中点.
(1)求证: 平面
平面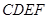 ;
;
(2)求多面体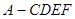 的体积.
的体积.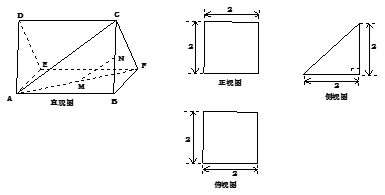
2008年5月12日,四川汶川发生8.0级特大地震,通往灾区的道路全部中断. 5月12日晚,抗震救灾指挥部决定从水路(一支队伍)、陆路(东南和西北两个方向各一支队伍)和空中(一支队伍)同时向灾区挺进.在5月13日,仍时有较强余震发生,天气状况也不利于空中航行. 已知当天从水路抵达灾区的概率是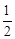 ,从陆路每个方向抵达灾区的概率都是
,从陆路每个方向抵达灾区的概率都是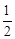 ,从空中抵达灾区的概率是
,从空中抵达灾区的概率是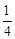 .
.
(1)求在5月13日恰有1支队伍抵达灾区的概率;
(2)求在5月13日抵达灾区的队伍数 的数学期望.
的数学期望.
在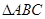 中,
中,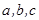 分别是角A、B、C的对边,
分别是角A、B、C的对边, 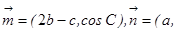
 ,且
,且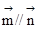 .
.
(1)求角A的大小;
(2)求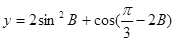 的值域.
的值域.