已知函数f(x)=alnx+bx,且f(1)=-1,f′(1)=0,
⑴求f(x);
⑵求f(x)的最大值;
⑶若x>0,y>0,证明:lnx+lny≤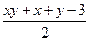 .
.
本题主要考查函数、导数的基本知识、函数性质的处理以及不等式的综合问题,同时考查考生用函数放缩的方法证明不等式的能力.
(本小题共12分)已知在等比数列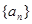 中,
中,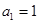 ,且
,且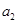 是
是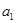 和
和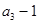 的等差中项.
的等差中项.
(1)求数列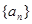 的通项公式;
的通项公式;
(2)若数列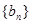 满足
满足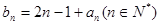 ,求
,求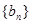 的前
的前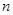 项和
项和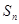 .
.
在△ABC中,a、b、c分别是角A、B、C的对边,且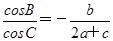 .
.
(1)求角B的大小;
(2)若b=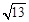 ,a+c=4,求△ABC的面积.
,a+c=4,求△ABC的面积.
(本小题满分12分) 已知关于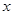 的不等式
的不等式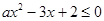 的解集为
的解集为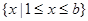 .
.
(1)求实数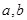 的值;
的值;
(2)解关于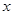 的不等式:
的不等式: (
( 为常数).
为常数).
(本小题满分10分)已知命题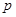 :方程
:方程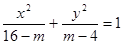 表示焦点在
表示焦点在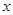 轴上的椭圆;命题
轴上的椭圆;命题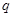 :点
:点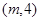 在圆
在圆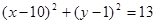 内.若
内.若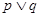 为真命题,
为真命题,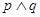 为假命题,试求实数
为假命题,试求实数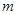 的取值范围.
的取值范围.
已知椭圆C: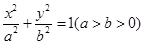 的两焦点与短轴的一个端点的连线构成等腰直角三角形,直线
的两焦点与短轴的一个端点的连线构成等腰直角三角形,直线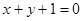 与以椭圆C的右焦点为圆心,以
与以椭圆C的右焦点为圆心,以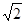
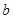 为半径的圆相切.
为半径的圆相切.
(1)求椭圆的方程.
(2)若过椭圆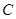 的右焦点
的右焦点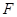 作直线
作直线 交椭圆
交椭圆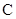 于
于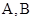 两点,交y轴于
两点,交y轴于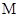 点,且
点,且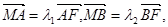 求证:
求证: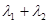 为定值
为定值