已知函数 ,
,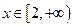 .
.
(Ⅰ)当 时,求函数
时,求函数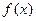 的最小值;
的最小值;
(Ⅱ)若对任意的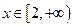 ,
,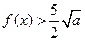 恒成立,求正实数
恒成立,求正实数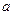 的取值范围.
的取值范围.
面上有9个红点,5个黄点,其中有2个红点和2个黄点在一条直线上,其余再无任何三点共线,问以这些点为三角形的顶点,其中三个顶点的颜色不完全相同的三角形有多少个?
一份考卷有10道考题,分为A、B两组,每组5题,要求考生选答6题,但每组最多选4题,问考生有几种选答方式?
从5双不同的鞋子中任取4只,
(1)取出的4只鞋子中至少能配成1双,有多少种不同的取法?
(2)取出的4只鞋子,任何两只都不能配成1双,有多少种不同的取法?
用正五棱柱的10个顶点中的5个顶点作四棱锥的5个顶点,共可得多少个四棱锥?
某商场为促销设计两套方案:(1)全场九折;(2)购物100元摸彩球打折,8个红色和8个绿色的玻璃球放在一个盒子里,顾客任意摸出8个球,仅有抽出的红球、绿球个数相等时不打折,两者相差一个时打9折,两者相差2个或2个以上时打8折,问商场应选择哪种方案更有利可图?