（本小题满分14分）
为了调查老年人的身体状况，某老年活动中心对80位男性老年人和100位女性老年人在一次慢跑后的心率水平作了记录，记录结果如下列两个表格所示，
表1：80位男性老年人的心率水平的频数分布表（单位：次/分钟）
| 心率水平 |
 |
 |
 |
 |
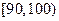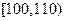| 频数 |
10 |
40 |
20 |
10 |
表2：100位女性老年人的心率水平的频数分布表（单位：次/分钟）
| 心率水平 |
|
|
|
|
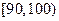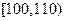| 频数 |
10 |
20 |
50 |
20 |
（1）从100位女性老人中任抽取两位作进一步的检查，求抽到的两位老人心率水平都在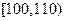内的概率；
（2）根据表2，完成下面的频率分布直方图，并由此估计这100女性老人心率水平的中位数；
（3）完成下面2×2列联表，并回答能否在犯错误的概率不超过0.001的前提下认为“这180位老人的心率水平是否低于100与性别有关”.
表3：
| 心率水平 性别 |
心率小于100 |
心率大于或等于100 |
合计 |
| 男性 |
 |
 |
|
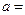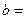| 女性 |
 |
 |
|
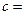| 合计 |
|
|
 |
附：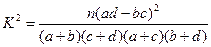
 |
 |
 |
 |
 |
 |
 |
 |
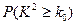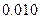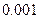已知f(x)定义在R上的偶函数，在区间
上递增，且有
,求a的取值范围.
(1)化简：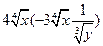
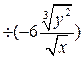
(2)计算：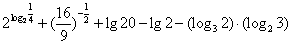
探究函数
，
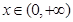的最小值，并确定取得最小值时
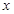的值，列表如下：
|
… |
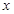0.5 |
1 |
1.5 |
1.7 |
1.9 |
2 |
2.1 |
2.2 |
2.3 |
3 |
4 |
5 |
7 |
… |
 |
… |
8.5 |
5 |
4.17 |
4.05 |
4.005 |
4 |
4.005 |
4.102 |
4.24 |
4.3 |
5 |
5.8 |
7.57 |
… |
请观察表中值随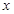值变化的特点，完成下列问题：
(1) 当
时，在区间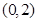
上递减，在区间上递增；
所以，
=时, 取到最小值为；
(2) 由此可推断，当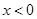
时，有最值为，此时=；
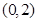(3) 证明： 函数在区间上递减；
(4) 若方程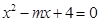
在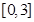
内有两个不相等的实数根，求实数
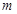的取值范围。
已知二次函数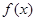
的二次项系数为
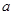，且不等式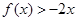
的解集为
。
（Ⅰ）若方程
有两个相等的根，求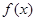的解析式；
（Ⅱ）若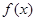的最大值为正数，求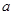的取值范围。
已知函数
（1）求
的解析式及定义域；
（2）求的最大值和最小值。