如图,已知四棱锥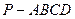 中,底面
中,底面 是直角梯形,
是直角梯形, ,
,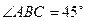 ,
,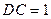 ,
,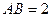 ,
, 平面
平面 ,
, .
. 
(1)求证: 平面
平面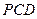 ;
;
(2)求证: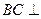 平面
平面 ;
;
(3)若M是PC的中点,求三棱锥M—ACD的体积.
.甲、乙两射击运动员进行射击比赛,射击次数相同,已知两运动员击中的环数 稳定在7,8,
稳定在7,8,
9,10环,他们比赛成绩的频率分布 直方图如下:(如果将频率近似的看作概率)
直方图如下:(如果将频率近似的看作概率)
(1)估计乙运动员击中8环的概率,并求甲、乙同时击中9环以上(包括9环)的概率;
(2)求甲运动员击中环数 的概率分布列及期望;若从甲、乙运动员中只能挑选一名参加某大型比赛,你认为让谁参加比较合适?
的概率分布列及期望;若从甲、乙运动员中只能挑选一名参加某大型比赛,你认为让谁参加比较合适?
 已知
已知 ,其中向量
,其中向量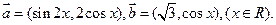
(1)求 的最小正周期和最小值;
的最小正周期和最小值;
(2)在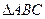 中,角A、B、C的对边分
中,角A、B、C的对边分 别为a、b、c,若
别为a、b、c,若 求边长c的值。
求边长c的值。
(本小题满分 14分)已知数列
14分)已知数列 是以
是以 d为公差的等差数列,数列
d为公差的等差数列,数列 是以q为公比的
是以q为公比的
等比数列。
(1)若数列 的前n项和为
的前n项和为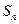 且
且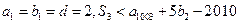 ,求整数q的值;
,求整数q的值;
(2)在(1)的条件下,试问数列 中最否存在一项
中最否存在一项 ,使得
,使得 恰好可以表示为该数列
恰好可以表示为该数列
中连续 项的和?请说明理由;
项的和?请说明理由;
(3)若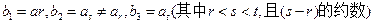 ,求证:数列
,求证:数列
中每一项都是数列 中的项。
中的项。
((本小题满分13分 )已知函数
)已知函数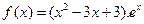 ,设
,设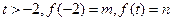 。
。
(1)试确定 的取值范围,使得函数
的取值范围,使得函数 在
在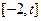 上为单调函数;
上为单调函数;
(2)试判断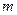 、
、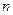 的大小并说明理由;
的大小并说明理由;
(3)求证:对于任意的 ,总存在
,总存在 ,满足
,满足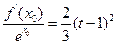 ,并确定这样的
,并确定这样的 的个数。
的个数。
((本小题满分12分)设椭圆 的焦点分别为
的焦点分别为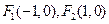 ,
,
直线 交
交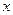 轴于于点A,且
轴于于点A,且 。
。
(1)试求椭圆的方程;
(2)过 、
、 分别作互相垂直的两直线与椭圆分别
分别作互相垂直的两直线与椭圆分别
交于D、E、M、N四点(如图所示),若四边形
DMEN的面积为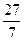 ,求DE的直线方程。
,求DE的直线方程。