先化简,再求值: ,其中
,其中
解不等式:
.解不等式 ,
, 并把它的解集在数轴上表示出来.
并把它的解集在数轴上表示出来.
.如图1,在平面直角坐标系xOy中, 矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上
矩形OABC的边OA在y轴的正半轴上,OC在x轴的正半轴上
 ,OA=1,OC=2,
,OA=1,OC=2, 点D在边OC上且
点D在边OC上且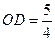 .
.
(1)求直线AC的解析式;
(2)在 y轴上
y轴上 是否存在点P,直线PD与矩形对角线AC交于点M,使得
是否存在点P,直线PD与矩形对角线AC交于点M,使得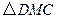 为等腰三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
为等腰三角形?若存在,直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
(3) 抛物线
抛物线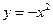 经过怎样平移,才能使得平移后的抛物线过点D和点E(点E在y轴正半轴上),且
经过怎样平移,才能使得平移后的抛物线过点D和点E(点E在y轴正半轴上),且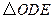 沿DE折叠后点O落在边AB上
沿DE折叠后点O落在边AB上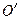 处?
处?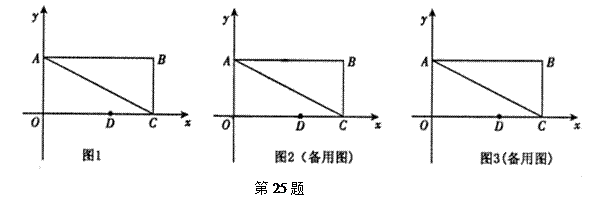
.在一个不透明的盒子里,装有四个分别标有数字1,2,3,4的小球,它们的形状、大小、质地等完全相同.小明先从盒子里随机取出一个小球,记下数字为x;放回盒子摇匀后,再由小华随机取出一个小球,记下数字为y.
(1)用列表法表示出(x,y)的所有可能出现的结果;
(2)求小明、小华各取一次小球所确定的点(x,y)落在反比例函数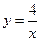 的图象上的概率;
的图象上的概率;
(3)求小明、小华 各取一次小球所确定的数x、y满足
各取一次小球所确定的数x、y满足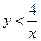 的概率.
的概率.
.如图,A、B是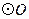 上的两点,
上的两点,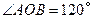 ,点D为劣弧
,点D为劣弧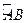 的中点.
的中点.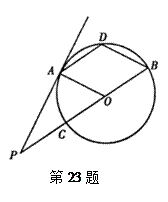
(1)求证:四边形AOB D是菱形;
D是菱形;
(2)延长线段BO至点P,交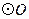 于另一点C,且BP=3OB,求证:AP是
于另一点C,且BP=3OB,求证:AP是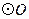 的切线.
的切线.