如图8,在Rt△ABC中,∠ACB=90°, ∠B=60°,BC=2.点O是AC的中点,过点O的直线l从与AC重合的位置开始,绕点O作逆时针旋转,交AB边于点D.过点C作CE∥AB交直线l于点E,设直线l的旋转角为α. 
解答下列问题:
(1) ① 当α=________度时,四边形EDBC是直角梯形;
② 当α=________度时,四边形EDBC是等腰梯形,此时AD的长为_________;
(2) 当α=90°时,判断四边形EDBC是否为菱形,并说明理由.
如图,AB为⊙O的直径,点C在⊙O上,延长BC至点D,使DC=CB,延长DA与⊙O的另一个交点为E,连接AC,CE.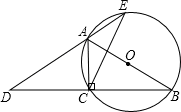
(1)求证:∠B=∠D;
(2)若AB=4,BC﹣AC=2,求CE的长.
如图,在矩形ABCD中,AB=6cm,BC=12cm,点P从点A沿边AB向点B以1cm/s的速度移动;同时,点Q从点B沿边BC向点C以2cm/s的速度移动,有一点到终点运动即停止.问: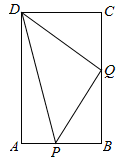
(1)几秒钟后△PBQ的面积等于8cm2?
(2)几秒钟后PQ⊥DQ?
(3)是否存在这样的时刻,使S△PDQ=8cm2,试说明理由.
如图,在半径为5的扇形 中,
中, =90°,点
=90°,点 是弧
是弧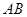 上的一个动点(不与点
上的一个动点(不与点 、
、 重合)
重合) ,
,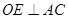 ,垂足分别为
,垂足分别为 、
、 .
.
(1)当BC=6时,求线段 的长;
的长;
(2)在 中是否存在长度保持不变的边?如果存在,请指出并求其长度,如果不存在,请说明理由;
中是否存在长度保持不变的边?如果存在,请指出并求其长度,如果不存在,请说明理由;
如图:已知P是半径为5cm的⊙O内一点.解答下列问题: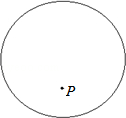
(1)用尺规作图找出圆心O的位置.(要求:保留所有的作图痕迹,不写作法)
(2)用三角板分别画出过点P的最长弦AB和最短弦CD.
(3)已知OP=3cm,过点P的弦中,长度为整数的弦共有_________ 条.
某商场销售一批名牌衬衫,平均每天可售出20件,每件赢利40元,为了扩大销售,增加赢利,尽快减少库存,商场决定采取适当的降价措施,经调查发现,如果每件衬衫每降价1元,商场平均每天可多售出2件。求:
(1)若商场平均每天要赢利1200元,每件衬衫应降价多少元?
(2)每件衬衫降价多少元时,商场平均每天赢利最多?