(本小题满分12分)
如图, 在直三棱柱ABC-A1B1C1中,AC=3 ,BC=4,
,BC=4, ,AA1=4,点D是AB的中点.
,AA1=4,点D是AB的中点.
(Ⅰ)求证:AC⊥BC1;
(Ⅱ)求二面角 的余弦值.
的余弦值.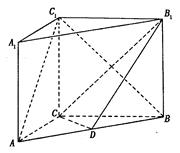
(本小题满分12分)已知广东省某校高三(1)班有 名学生,从中按系统抽样抽取
名学生,从中按系统抽样抽取 名学生.
名学生.
(Ⅰ)若第 组抽出的号码为
组抽出的号码为 ,写出所有被抽出学生的号码;
,写出所有被抽出学生的号码;
(Ⅱ)分别统计这 名学生的某高校自主招生考试成绩(满分:
名学生的某高校自主招生考试成绩(满分: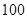 分),获得成绩数据的茎叶图如图所示,现从这
分),获得成绩数据的茎叶图如图所示,现从这 名学生中随机抽取两名成绩超过平均分的学生,求成绩为
名学生中随机抽取两名成绩超过平均分的学生,求成绩为 分的学生被抽取到的概率.
分的学生被抽取到的概率.
(本小题满分12分)已知函数 ,
, .
.
(Ⅰ)求 的值;
的值;
(Ⅱ)设 ,
, ,
, ,
, ,求
,求 的值.
的值.
(坐标系与参数方程选做题)在直角坐标系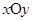 中,圆
中,圆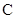 的参数方程是
的参数方程是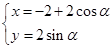 (
( 为参数),若以点
为参数),若以点 为极点,
为极点, 轴正半轴为极轴建立极坐标系,则圆心
轴正半轴为极轴建立极坐标系,则圆心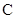 的极坐标是 .
的极坐标是 .
(本小题满分14分)设函数
 .
.
(1)当函数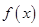 在定义域内为增函数时,求
在定义域内为增函数时,求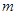 的取值范围;
的取值范围;
(2)设 是曲线
是曲线 上的两个不同点,且曲线在
上的两个不同点,且曲线在 两点处的切线均与
两点处的切线均与 轴平行,直线
轴平行,直线 的斜率为
的斜率为 ,是否存在
,是否存在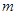 使得
使得 ,若存在,请求出
,若存在,请求出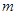 的值,若不存在,请说明理由.
的值,若不存在,请说明理由.
(本小题满分14分)设递增数列 满足
满足 ,
, 且
且 .
.
(1)证明:数列 是等差数列;
是等差数列;
(2)设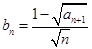 ,记数列
,记数列 的前
的前 项和为
项和为 ,使得不等式
,使得不等式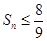 成立的最大正整数
成立的最大正整数 的值.
的值.