一汽车厂生产A,B,C三类轿车,每类轿车均有舒适型和标准型两种型号,某月的产量如下表(单位:辆):
| |
轿车A |
轿车B |
轿车C |
| 舒适型 |
100 |
150 |
z |
| 标准型 |
300 |
450 |
600 |
按类型分层抽样的方法在这个月生产的轿车中抽取50辆,其中有A类轿车10辆.
(1) 求z的值. 

(2) 用分层抽样的方法在C类轿车中抽取一个容量为5的样本.将该样本看成一个总体,从中任取2辆,求至少有1辆舒适型轿车的概率;
(3) 用随机抽样的方法从B类舒适型轿车中抽取8辆,经检测它们的得分如下:9.4, 8.6, 9.2, 9.6, 8.7, 9.3, 9.0, 8.2.把这8辆轿车的得分看作一个总体,从中任取一个数,求该数与样本平均数之差的绝对值不超过0.5的概率.
(本小题满分10分)选修4-5:不等式选讲
已知函数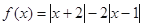
(1)解不等式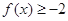 ;
;
(2)对任意 ,都有
,都有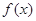
 成立,求实数
成立,求实数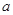 的取值范围.
的取值范围.
(本小题满分14分)已知函数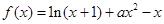 (
(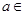 R).
R).
(1)当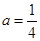 时,求函数
时,求函数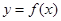 的单调区间;
的单调区间;
(2)若对任意实数 ,当
,当 时,函数
时,函数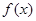 的最大值为
的最大值为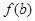 ,求
,求 的取值范围.
的取值范围.
(本小题满分12分)如图所示,桶1中的水按一定规律流入桶2中,已知开始时桶1中有 升水,桶2是空的,
升水,桶2是空的, 分钟后桶1中剩余的水量符合指数衰减曲线
分钟后桶1中剩余的水量符合指数衰减曲线 (其中
(其中 是常数,
是常数, 是自然对数的底数).假设在经过5分钟时,桶1和桶2中的水恰好相等.求:
是自然对数的底数).假设在经过5分钟时,桶1和桶2中的水恰好相等.求:
(1)桶2中的水 (升)与时间
(升)与时间 (分钟)的函数关系式;
(分钟)的函数关系式;
(2)再过多少分钟,桶1中的水是 升?
升?
(本小题满分12分)已知正项等差数列 的前
的前 项和为
项和为 ,且满足
,且满足 ,
, .
.
(1)求数列 的通项公式;
的通项公式;
(2)若数列 满足
满足 ,
, ,求数列
,求数列 的前
的前 项和
项和 .
.
(本小题满分12分)在 中,设角
中,设角 的对边分别为
的对边分别为 ,且
,且 .
.
(1)求角 的大小;
的大小;
(2)若 ,求边
,求边 的大小.
的大小.