已知椭圆的两焦点为 ,
,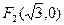 ,离心率
,离心率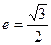 .(1)求此椭圆的方程;(2)设直线
.(1)求此椭圆的方程;(2)设直线 ,若
,若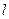 与此椭圆相交于
与此椭圆相交于 ,
,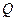 两点,且
两点,且 等于椭圆的短轴长,求
等于椭圆的短轴长,求 的值;
的值;
为了了解某市工厂开展群众体育活动的情况,拟采用分层抽样的方法从 三个区中抽取6个工厂进行调查.已知
三个区中抽取6个工厂进行调查.已知 区中分别有27,18,9个工厂.
区中分别有27,18,9个工厂.
(Ⅰ)求从 区中应分别抽取的工厂个数;
区中应分别抽取的工厂个数;
(Ⅱ)若从抽得的6个工厂中随机地抽取2个进行调查结果的对比,求这2个工厂中至少有1个来自 区的概率.
区的概率.
在 中,角
中,角 ,
, ,
, 的对边为
的对边为 ,
, ,
, 且;
且;
(Ⅰ)求 的值;
的值;
(Ⅱ)若 ,
, ,求
,求 的值.
的值.
已知坐标平面内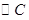 :
: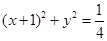 ,
, :
: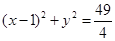 .动点P与
.动点P与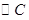 外切与
外切与 内切.
内切.
(1)求动圆心P的轨迹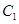 的方程;
的方程;
(2)若过D点的斜率为2的直线与曲线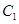 交于两点A、B,求AB的长;
交于两点A、B,求AB的长;
(3)过D的动直线与曲线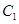 交于A、B两点,线段中点为M,求M的轨迹方程.
交于A、B两点,线段中点为M,求M的轨迹方程.
设进入某商场的每一位顾客购买甲种商品的概率为0.5,购买乙种商品的概率为0.6, 且购买甲种商品与购买乙种商品相互独立,各顾客之间购买商品也是相互独立的.
(1)求进入商场的1位顾客至少购买甲、乙两种商品中的一种的概率;
(2)记 表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求
表示进入商场的3位顾客中至少购买甲、乙两种商品中的一种的人数,求 的分布列及期望.
的分布列及期望.
(1)求 的展开式中的常数项;
的展开式中的常数项;
(2)已知 ,
,
求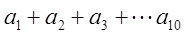 的值.
的值.