各棱长均为2的斜三棱柱ABC—DEF中，已知BF⊥AE，
BF∩CE=O，AB=AE，连结AO。
（I）求证：AO⊥平面FEBC。
（II）求二面角B—A
C—E的大小。
（III）求三棱锥B—DEF的体积。
已知：集合M是满足下列性质的函数f（x）的全体：在定义域内存在x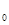
，使得
f（x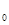＋1）＝f（x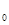）＋f（1）成立。
（1）函数f（x）＝
是否属于集合M？说明理由；
（2）设函数f（x）＝lg
，求实数a的取值范围；
（3）证明：函数f（x）＝2
＋x
M。
已知：函数f（x）＝ax（0<a<1），
（Ⅰ）若f（x
）＝2，求f（3x）；
（Ⅱ）若f（2x
－3x＋1）
f（x＋2x－5），求x的取值范围。
已知：函数f（x）＝
，x
，
（1）当a＝－1时，判断并证明函数的单调性并求f（x）的最小值；
（2）若对任意x，f（x）>0都成立，试求实数a的取值范围。
已知：函数f（x）＝x
－bx＋3，且f（0）＝f（4）。
（1）求函数y＝f（x）的零点，写出满足条件f（x）<0的x的集合；
（2）求函数y＝f（x）在区间[0，3]上的最大值和最小值。
已知：函数f（x）＝
＋lg（3
－9）的定义域为A，集合B＝
，
（1）求：集合A；
（2）求：A
B。