已知：函数f（x）＝x
－bx＋3，且f（0）＝f（4）。
（1）求函数y＝f（x）的零点，写出满足条件f（x）<0的x的集合；
（2）求函数y＝f（x）在区间[0，3]上的最大值和最小值。
已知椭圆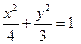
，试确定
的值，使得在此椭圆上存在不同
两点关于直线
对称。
已知数列
中，
，前
项和为
（I）证明数列
是等差数列，并求出数列的通项公式；
（II）设
，数列
的前项和为
，求使不等式
对一切
都成立的最大正整数
的值。
数列
满足：
（1）求数列
的通项公式；
（2）设数列的前n项和分别为An、Bn，问是否存在实数
，使得
为等差数列？若存在，求出的值；若不存在，说明理由。
已知
、
、
为
的三内角，且其对边分别为
、
、
，若
．
（1）求；
（2）若
，求的面积．
已知双曲线的中心在原点，焦点在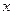
轴上，离心率
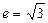，焦距为
（1）求该双曲线方程.
（2）是否定存在过点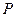
，
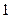）的直线
与该双曲线交于
，
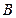两点，且点
是线段
的中点？若存在，请求出直线的方程，若不存在，说明理由.