已知双曲线的中心在原点,焦点在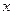 轴上,离心率
轴上,离心率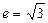 ,焦距为
,焦距为
(1)求该双曲线方程.
(2)是否定存在过点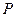
 ,
,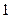 )的直线
)的直线 与该双曲线交于
与该双曲线交于 ,
,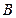 两点,且点
两点,且点 是线段
是线段 的中点?若存在,请求出直线
的中点?若存在,请求出直线 的方程,若不存在,说明理由.
的方程,若不存在,说明理由.
为了了解青少年视力情况,某市从高考体检中随机抽取16名学生的视力进行调查,经医生用对数视力表检查得到每个学生的视力状况的茎叶图(以小数点前的一位数字为茎,小数点后的一位数字为叶)如下: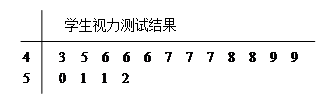
(1)若视力测试结果不低丁5.0,则称为“好视力”,求校医从这16人中随机选取3人,至多有1人是“好视力”的概率;
(2)以这16人的样本数据来估计该市所有参加高考学生的的总体数据,若从该市参加高考的学生中任选3人,记 表示抽到“好视力”学生的人数,求
表示抽到“好视力”学生的人数,求 的分布列及数学期望.
的分布列及数学期望.
已知曲线C的极坐标方程为 .
.
(1)若直线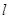 过原点,且被曲线C截得弦长最短,求此时直线
过原点,且被曲线C截得弦长最短,求此时直线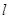 的标准形式的参数方程;
的标准形式的参数方程;
(2) 是曲线C上的动点,求
是曲线C上的动点,求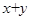 的最大值.
的最大值.
已知函数
(1).求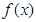 的周期和单调递增区间;
的周期和单调递增区间;
(2).若关于x的方程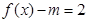 在
在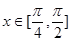 上有解,求实数m的取值范围.
上有解,求实数m的取值范围.
已知全集U=R,集合 ,函数
,函数 的定义域为集合B.
的定义域为集合B.
(1)若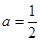 时,求集合
时,求集合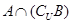 ;
;
(2)命题P:  ,命题q:
,命题q: 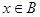 ,若q是p的必要条件,求实数a的取值范围.
,若q是p的必要条件,求实数a的取值范围.
已知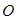 为坐标原点,
为坐标原点,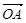 =(
=(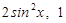 ),
),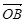 =(1,
=(1,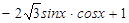 ),
),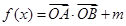 .
.
(1)若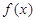 的定义域为[-
的定义域为[- ,
,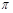 ],求y=
],求y=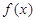 的单调递增区间;
的单调递增区间;
(2)若 的定义域为[
的定义域为[ ,
,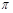 ],值域为[2,5],求
],值域为[2,5],求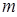 的值.
的值.