(满分14分)本题有2小题,第1小题6分,第2小题8分.
已知在平面直角坐标系 中,
中, 三个顶点的直角坐标分别为
三个顶点的直角坐标分别为 ,
, ,
, .
.
(1)若 ,求
,求 的值;
的值;
(2)若 为锐角三角形,求
为锐角三角形,求 的取值范围.
的取值范围.
如图,直角三角形 的顶点坐标
的顶点坐标 ,直角顶点
,直角顶点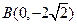 ,顶点
,顶点 在
在 轴上,点
轴上,点 为线段
为线段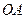 的中点
的中点
(1)求 边所在直线方程;(2)圆
边所在直线方程;(2)圆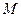 是△ABC的外接圆,求圆
是△ABC的外接圆,求圆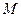 的方程;
的方程;
(3)若DE是圆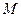 的任一条直径,试探究
的任一条直径,试探究 是否是定值?
是否是定值?
若是,求出定值;若不是,请说明理由.
求函数 的值域及y取得最小值时x的取值的集合.
的值域及y取得最小值时x的取值的集合.
在等比数列 中
中 ,求
,求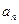 及前
及前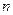 项和
项和 .
.
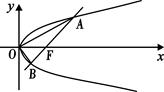
过直角坐标平面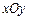 中的抛物线
中的抛物线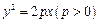 的焦点
的焦点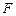 作一条倾斜角为
作一条倾斜角为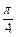 的直线与抛物线相交于A、B两点.
的直线与抛物线相交于A、B两点.
(1)求直线AB的方程;
(2)试用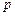 表示A、B之间的距离;
表示A、B之间的距离;
(3)当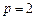 时,求
时,求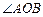 的余弦值.
的余弦值.
参考公式: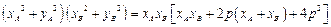 .
.
已知函数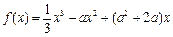 ,
, .
.
(1)当 时,求
时,求 在闭区间
在闭区间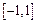 上的最大值与最小值;
上的最大值与最小值;
(2)若线段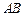 :
: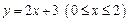 与导函数
与导函数 的图像只有一个交点,且交点在线段
的图像只有一个交点,且交点在线段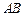 的内部,试求
的内部,试求 的取值范围.
的取值范围.