如图,直角三角形 的顶点坐标
的顶点坐标 ,直角顶点
,直角顶点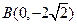 ,顶点
,顶点 在
在 轴上,点
轴上,点 为线段
为线段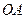 的中点
的中点
(1)求 边所在直线方程;(2)圆
边所在直线方程;(2)圆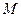 是△ABC的外接圆,求圆
是△ABC的外接圆,求圆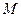 的方程;
的方程;
(3)若DE是圆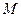 的任一条直径,试探究
的任一条直径,试探究 是否是定值?
是否是定值?
若是,求出定值;若不是,请说明理由.
(本小题14 分)
已知函数 .
.
①当 时,求
时,求 的最小值;
的最小值;
②若函数 在区间
在区间 上为单调函数,求实数
上为单调函数,求实数 的取值范围;
的取值范围;
③当 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.
(本小题13分)
已知抛物线方程为 ,过
,过 作直线
作直线 .
.
①若 与
与 轴不垂直,交抛物线于A、B两点,是否存在
轴不垂直,交抛物线于A、B两点,是否存在 轴上一定点
轴上一定点 ,使得
,使得 ?若存在,求出m的值;若不存在,请说
?若存在,求出m的值;若不存在,请说 明理由?
明理由?
②若 与
与 轴垂直,抛物线的任一切线与
轴垂直,抛物线的任一切线与 轴和
轴和 分别交于M、N两点,则自点M到以QN为直径的圆的切线长
分别交于M、N两点,则自点M到以QN为直径的圆的切线长 为定值,试证之;
为定值,试证之;
.(本小题12分)
已知数列 ,
, 分别是等差、等比数列,且
分别是等差、等比数列,且 ,
, ,
, .
.
①求数列 ,
, 的通项公式;
的通项公式;
②设 为数列
为数列 的前
的前 项和,求
项和,求 的前
的前 项和
项和 ;
;
③设 ,
, ,请效仿②的求和方法,求
,请效仿②的求和方法,求 .
.
.(本小题12 分)如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且与底面ABCD垂直,底面ABCD为正方形,E、F分别为AB、PC的中点.
①求证:EF⊥平面PCD;
②求平面PCB与平面PCD的夹角的余弦值.
.(本小题12 分)
有一个箱子内放有3个红球、1个白球、1个黄球,现从箱子里任意取球,每次只取一个,取后不放回.
①求前两次先后取到一个红球和一个白球的概率;
②若取得红球则停止取球,求取球次数 的分布列及期望.
的分布列及期望.