(本小题满分12分)
已知数列{an}和{bn}满足: a1= ,an+1=
,an+1= an+n-4,bn=(-1)n(an-3n+21),其中
an+n-4,bn=(-1)n(an-3n+21),其中 为实数,n为正整数.
为实数,n为正整数.
(Ⅰ)证明:对 任意实数
任意实数 ,数列{an}不是等比数列;
,数列{an}不是等比数列;
(Ⅱ)证明:当 ≠-18时,数列{bn}是等比数列.
≠-18时,数列{bn}是等比数列.
(本题满分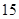 分)已知抛物线
分)已知抛物线 :
: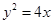 ,过
,过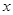 轴上的一定点
轴上的一定点 的直线
的直线 交抛物线
交抛物线 于
于 、
、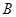 两点(
两点( 为大于零的正常数).
为大于零的正常数).
(1)设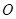 为坐标原点,求
为坐标原点,求 面积的最小值;
面积的最小值;
(2)若点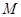 为直线
为直线 上任意一点,探求:直线
上任意一点,探求:直线 的斜率是否成等差数列?若是,则给出证明;若不是,则说明理由.
的斜率是否成等差数列?若是,则给出证明;若不是,则说明理由.
(本小题满分15分)数列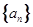 的前
的前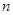 项和为
项和为 ,满足
,满足 ,数列
,数列 的前
的前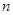 项和为
项和为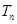 ,满足
,满足
 .
.
(1)求数列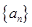 、
、 的通项公式;
的通项公式;
(2)若对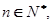 恒有
恒有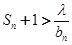 成立,求实数
成立,求实数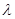 的取值范围.
的取值范围.
(本小题满分15分)如图所示,在四棱锥 中,底面
中,底面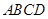 是矩形,侧棱
是矩形,侧棱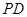 ⊥底面
⊥底面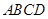 ,
, ,
,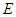 是
是 的中点,作
的中点,作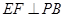 交
交 于点
于点 .
.
(1)证明: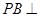 平面
平面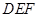 ;
;
(2)若 ,求直线
,求直线 与平面
与平面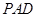 所成角的正弦值.
所成角的正弦值.
(本小题满分15分)已知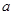 ,
,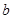 ,
, 分别是
分别是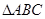 的内角
的内角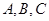 所对的边,且
所对的边,且 ,
, .
.
(1)求角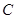 的大小;
的大小;
(2)若 ,求边
,求边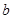 的长.
的长.
现有甲类产品有4件,乙类产品有3件,丙类产品有2件,将这些产品随机排成一列,则同类产品不相邻的排法有几种?