如图, 、
、 两座城市相距100千米,现计划在这两座城市之间修筑一条高等级公路(即线段
两座城市相距100千米,现计划在这两座城市之间修筑一条高等级公路(即线段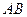 )。经测量,森林保护区中心
)。经测量,森林保护区中心 点在
点在 城市的北偏东30°方向,
城市的北偏东30°方向, 城市的北偏西45°方向上,已知森林保护区的范围在以
城市的北偏西45°方向上,已知森林保护区的范围在以 为圆心,50千米为半径的圆形区域内。请问:计划修筑的这条高等级公路会不会穿越保护区,为什么?
为圆心,50千米为半径的圆形区域内。请问:计划修筑的这条高等级公路会不会穿越保护区,为什么?
公差不为0的等差数列 中,
中, 且
且 成等比数列.
成等比数列.
(I)求数列 的通项公式和它的前20项和
的通项公式和它的前20项和 .
.
(II) 求数列 前n项的和
前n项的和 .
.
已知集合 ,集合
,集合 ,
,
集合
(Ⅰ)求 ;(Ⅱ)若
;(Ⅱ)若 ,试确定实数
,试确定实数 的取值范围.
的取值范围.
国家教育部、体育总局和共青团中央曾共同号召,在全国各级各类学校要广泛、深入地开展全国亿万大中小学生阳光体育运动.为此某网站于2010年1月18日至24日,在全国范围内进行了持续一周的在线调查,随机抽取其中200名大中小学生的调查情况,就每天的睡眠时间分组整理如下表所示:
序号( ) ) |
每天睡眠时间 (小时) |
组中值( ) ) |
频数 |
频率 (  ) ) |
| 1 |
[4,5) |
4.5 |
8 |
0.04 |
| 2 |
[5,6) |
5.5 |
52 |
0.26 |
| 3 |
[6,7) |
6.5 |
60 |
0.30 |
| 4 |
[7,8) |
7.5 |
56 |
0.28 |
| 5 |
[8,9) |
8.5 |
20 |
0.10 |
| 6 |
[9,10) |
9.5 |
4 |
0.02 |
 |
(Ⅰ)估计每天睡眠时间小于8小时的学生所占的百分比约是多少;
(Ⅱ)该网站利用上面的算法流程图,对样本数据作进一步统计
分析,求输出的S的值,并说明S的统计意义.
已知甲、乙、丙三种食物的维生素A、B含量及成本如下表:
| 甲 |
乙 |
丙 |
|
| 维生素A(单位/kg) |
60 |
70 |
40 |
| 维生素B(单位/kg) |
80 |
40 |
50 |
| 成本(元/kg) |
11 |
9 |
4 |
现分别用甲、乙、丙三种食物配成10kg混合食物,并使混合食物内至少含有560单位维生素A和630单位维生素B.
(Ⅰ)若混合食物中恰含580单位维生素A和660单位维生素B,求混合食物的成本为多少元?
(Ⅱ)分别用甲、乙、丙三种食物各多少kg,才能使混合食物的成本最低?最低成本为多少元?
已知定义在R上的函数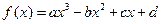 (a,b,c,d为实常数)的图象关于原点对称,且当x=1时f(x)取得极值
(a,b,c,d为实常数)的图象关于原点对称,且当x=1时f(x)取得极值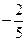 .
.
(Ⅰ)求函数f(x)的解析式;
(Ⅱ)证明:对任意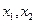 ∈[-1,1],不等式
∈[-1,1],不等式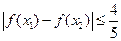 成立;
成立;
(Ⅲ)若函数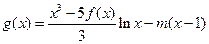 在区间(1,∞)内无零点,求实数m的取值范围.
在区间(1,∞)内无零点,求实数m的取值范围.