(此题8、9、10班做)(本小题满分13分)
设数列 的前
的前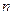 项和为
项和为 ,对一切
,对一切 ,点
,点 都在函数
都在函数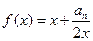 的图象上.
的图象上.
(Ⅰ)求 及数列
及数列 的通项公式
的通项公式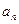 ;
;
(Ⅱ) 将数列 依次按1项、2项、3项、4项循环地分为(
依次按1项、2项、3项、4项循环地分为( ),(
),(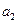 ,
, ),(
),(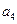 ,
,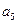 ,
, ),(
),( ,
,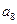 ,
,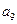 ,
,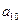 );(
);(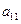 ),(
),(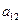 ,
,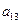 ),(
),( ,
,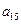 ,
, ),(
),( ,
, ,
, ,
,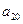 );(
);( ),…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为
),…,分别计算各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为 ,求
,求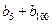 的值;
的值;
(Ⅲ)令 (
(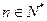 ),求证:
),求证: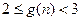 .
.
设数列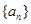 的前n项和为
的前n项和为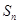 ,满足
,满足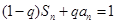 ,且
,且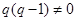 .
.
(Ⅰ)求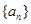 的通项公式;
的通项公式;
(Ⅱ)若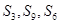 成等差数列,求证:
成等差数列,求证: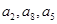 成等差数列.
成等差数列.
选修4-5:不等式选讲
已知函数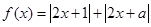
(Ⅰ)a=-3时,求不等式 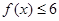 的解集;
的解集;
(Ⅱ)若关于x的不等式 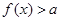 恒成立,求实数a的取值范围
恒成立,求实数a的取值范围
选修4-4:坐标系与参数方程
己知抛物线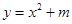 的顶点M到直线
的顶点M到直线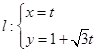 (t为参数)的距离为1
(t为参数)的距离为1
(1)求m;
(2)若直线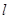 与抛物线相交于A,B两点,与y轴交于N点,求
与抛物线相交于A,B两点,与y轴交于N点,求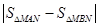 的值.
的值.
选修4-1:几何证明选讲
如图, 是
是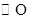 的一条切线,切点为
的一条切线,切点为 ,直线
,直线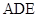 ,
,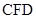 ,
,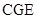 都是
都是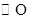 的割线,已知
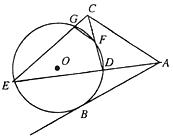
的割线,已知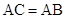 .
.
(1)求证: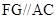 ;
;
(2)若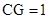 ,
,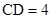 .求
.求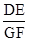 的值.
的值.
已知函数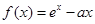 ,其中e为自然对数的底数,a为常数.
,其中e为自然对数的底数,a为常数.
(1)若对函数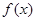 存在极小值,且极小值为0,求a的值;
存在极小值,且极小值为0,求a的值;
(2)若对任意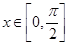 ,不等式
,不等式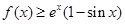 恒成立,求a的取值范围.
恒成立,求a的取值范围.