本题满分13分)
某食品厂进行蘑菇的深加工,每公斤蘑菇的成本20元,并且每公斤蘑菇的加工费为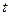 元(
元(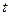 为常数,且
为常数,且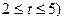 ,设该食品厂每公斤蘑菇的出厂价为
,设该食品厂每公斤蘑菇的出厂价为 元(
元(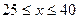 ),根据市场调查,销售量
),根据市场调查,销售量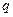 与
与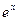 成反比,当每公斤蘑菇的出厂价为30元时,日销售量为100公斤.
成反比,当每公斤蘑菇的出厂价为30元时,日销售量为100公斤.
(Ⅰ)求该工厂的每日利润 元与每公斤蘑菇
元与每公斤蘑菇 的出厂价
的出厂价 元的函数关系式;
元的函数关系式;
(Ⅱ)若 ,当每公斤蘑菇的出厂价
,当每公斤蘑菇的出厂价 为多少元时,该工厂的利润
为多少元时,该工厂的利润 最大,并求最大值.
最大,并求最大值.
已知数列 满足
满足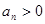 且对一切
且对一切 ,
,
有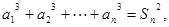
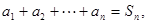
(Ⅰ)求证:对一切
(Ⅱ)求数列 通项公式.
通项公式.
(Ⅲ)求证:
已知椭圆
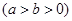 的离心率为
的离心率为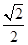 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线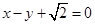 相切.
相切.
(I)求椭圆 的方程;
的方程;
(II)若过点 (2,0)的直线与椭圆
(2,0)的直线与椭圆 相交于两点
相交于两点 ,设
,设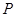 为椭圆上一点,且满足
为椭圆上一点,且满足 (O为坐标原点),当
(O为坐标原点),当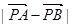 <
<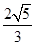 时,求实数
时,求实数 的取值范围.
的取值范围.
已知函数f(x)= ,
, 为常数。
为常数。
(I)当 =1时,求f(x)的单调区间;
=1时,求f(x)的单调区间;
(II)若函数f(x)在区间[1,2]上为单调函数,求 的取值范围。
的取值范围。
一个袋中装有四个形状大小完全相同的球,球的编号分别为1,2,3,4.
(I)从袋中随机抽取一个球,将其编号记为 ,然后从袋中余下的三个球中再随机抽取一个球,将其编号记为
,然后从袋中余下的三个球中再随机抽取一个球,将其编号记为 .求关于
.求关于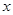 的一元二次方程
的一元二次方程 有实根的概率;
有实根的概率;
(II)先从袋中随机取一个球,该球的编号为m,将球放回袋中,然后再从袋中随机取一个球,该球的编号为n.若以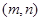 作为点P的坐标,求点P落在区域
作为点P的坐标,求点P落在区域 内的概率.
内的概率.
如图,在四棱锥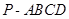 中,
中,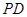 ⊥底面
⊥底面 ,底面
,底面 为正方形,
为正方形,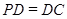 ,
,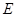 ,
, 分别是
分别是 ,
, 的中点.
的中点.
(I)求证: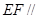 平面
平面 ;
;
(II)求证: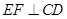 ;
;
(III)设PD="AD=a," 求三棱锥B-EFC的体积.