已知椭圆
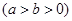 的离心率为
的离心率为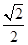 ,以原点为圆心,椭圆的短半轴长为半径的圆与直线
,以原点为圆心,椭圆的短半轴长为半径的圆与直线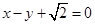 相切.
相切.
(I)求椭圆 的方程;
的方程;
(II)若过点 (2,0)的直线与椭圆
(2,0)的直线与椭圆 相交于两点
相交于两点 ,设
,设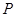 为椭圆上一点,且满足
为椭圆上一点,且满足 (O为坐标原点),当
(O为坐标原点),当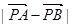 <
<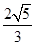 时,求实数
时,求实数 的取值范围.
的取值范围.
在每道单项选择题给出的4个备选答案中,只有一个是正确的.若对4道选择题中的每一道都任意选定一个答案,求这4道题中:
(1)恰有两道题答对的概率;
(2)至少答对一道题的概率。
7名师生站成一排照相留念,其中老师1人,男生4人,女生2人,在下列情况下,各有不同站法多少种?
(1)两中女生必须相邻而站;
(2)4名男生互不相邻;
(3)若4名男生身高都不等,按从高到低的一种顺序站;
(4)老师不站中间,女生不站两端.

在△ABC中,a、b、c分别为角A、B、C的对边,已知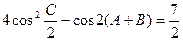 ,c=
,c=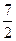 ,又△ABC的面积为S△ABC=
,又△ABC的面积为S△ABC= ,求a,b的值.
,求a,b的值.
设平面内有四个向量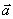 、
、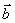 、
、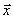 、
、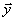 ,且满足
,且满足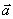 =
=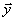 -
-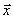 ,
, 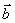 =2
=2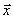 -
-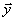 ,
,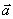 ⊥
⊥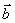 , |
, |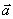 |=|
|=|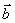 |=1
|=1
(1)求|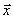 |,|
|,|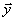 |;
|;
(2)若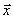 、
、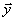 的夹角为
的夹角为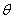 ,求cos
,求cos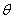 .
.
航空测量组的飞机航线和山顶在同一铅直平面内,已知飞机的高度为海拔10000m,速度为180km(千米)/h(小时)飞机先看到山顶的俯角为150,经过420s(秒)后又看到山顶的俯角为450,求山顶的海拔高度(取 =1.4,
=1.4,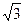 =1.7).
=1.7).
|
