(本小题满分14分)
设函数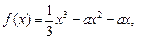
 .
.
(1) 试问函数f(x)能否在x=-1时取得极值?说明理由;
(2) 若a=-1,当x∈[-3,4]时,函数f(x)与g(x)的图像有两个公共点,求c的取值范围.
下图是一几何体的直观图、主视图、俯视图、左视图.
(1)若 为
为 的中点,求证:
的中点,求证:
 面
面 ;
;
(2)证明 面
面 .
.
(3)求该几何体的体积.
已知圆 的方程为
的方程为 ,直线
,直线 的方程为
的方程为 ,点
,点 在直线
在直线 上,过
上,过 点作圆
点作圆 的切线
的切线 ,切点为
,切点为 .
.
(1)若 ,试求点
,试求点 的坐标;
的坐标;
(2)若 点的坐标为
点的坐标为 ,过
,过 作直线与圆
作直线与圆 交于
交于 两点,当
两点,当 时,求直线
时,求直线 的方程;
的方程;
如图, 是圆柱体
是圆柱体 的一条母线,
的一条母线, 过底面圆的圆心
过底面圆的圆心 ,
, 是圆
是圆 上不与点
上不与点 、
、 重合的任意一点,已知棱
重合的任意一点,已知棱 ,
, ,
, .
.
(1)求证: ;
;
(2)将四面体 绕母线
绕母线 转动一周,求
转动一周,求 的三边在旋转过程中所围成的几何体的体积.
的三边在旋转过程中所围成的几何体的体积.
设x,y满足约束条件 ,
,
(1)画出不等式表示的平面区域,并求该平面区域的面积;
(2)若目标函数z=ax+by(a>0,b>0)的最大值为4,求 的最小值.
的最小值.
(1)求圆心在 轴上,且与直线
轴上,且与直线 相切于点
相切于点 的圆的方程;
的圆的方程;
(2)已知圆 过点
过点 ,且与圆
,且与圆 关于直线
关于直线 对称,求圆
对称,求圆 的方程.
的方程.