已知数列 中,
中,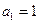 ,
,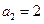 ,且
,且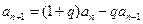
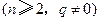 .
.
(1)设 ,证明
,证明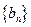 是等比数列;
是等比数列;
(2)求数列 的通项公式;
的通项公式;
已知平行四边形ABCD的两条对角线AC与BD交于E,O是任意一点,
求证: +
+ +
+ +
+ =4
=4
判断下列命题是否正确,若不正确,请简述理由.
①向量 与
与 是共线向量,则A、B、C、D四点必在一直线上;
是共线向量,则A、B、C、D四点必在一直线上;
②单位向量都相等;
③任一向量与它的相反向量不相等;
④四边形ABCD是平行四边形的充要条件是 =
=
⑤模为0是一个向量方向不确定的充要条件;
⑥共线的向量,若起点不同,则终点一定不同.
在平面直角坐标系中,O为坐标原点,已知向量 ,
,
又点
(1)若 且
且 ,求向量
,求向量 ;
;
(2)若向量 与向量
与向量 共线,当
共线,当 时,且
时,且 取最大值为4时,求
取最大值为4时,求
已知向量a是以点A(3,-1)为起点,且与向量b=(-3,4)
垂直的单位向量,求a的终点坐标
已知开口向上的二次函数f(x),对任意 ,恒有
,恒有 成立,设向量a=
成立,设向量a= ,b=(1,2)。
,b=(1,2)。
求不等式f(a·b)<f(5)的解集。