已知四棱锥 的底面为直角梯形,
的底面为直角梯形, ,
, 底面
底面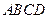 ,且
,且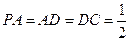 ,
, ,
,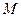 是
是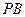 的
的 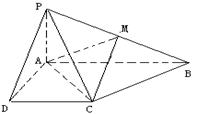
(Ⅰ)证明:面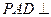 面
面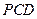 ;
;
(Ⅱ)求 与
与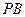 所成的角;
所成的角;
(Ⅲ)求面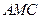 与面
与面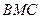 所成二面角的余弦值
所成二面角的余弦值
已知f(x)是偶函数,且f(x)在[0,+∞)上是增函数,若x∈ 时,不等式f(1+xlog2a)≤f(x-2)恒成立,求实数a的取值范围.
时,不等式f(1+xlog2a)≤f(x-2)恒成立,求实数a的取值范围.
已知定义在R上的函数f(x)对任意实数x、y恒有f(x)+f(y)=f(x+y),且当x>0时,f(x)<0,又f(1)=- .
.
(1)求证:f(x)为奇函数;
(2)求证:f(x)在R上是减函数;
(3)求f(x)在[-3,6]上的最大值与最小值.
设f(x)是定义在R上的奇函数,且对任意实数x,恒有f(x+2)=-f(x),当x∈[0,2]时,f(x)=2x-x2.
(1)求证:f(x)是周期函数;
(2)当x∈[2,4]时,求f(x)的解析式;
(3)计算f(0)+f(1)+f(2)+…+f(2014)的值.
已知奇函数f(x)的定义域为[-2,2],且在区间[-2,0]内递减,若f(1-m)+f(1-m2)<0,求实数m的取值范围.
已知函数f(x)= 是奇函数,求a+b的值;
是奇函数,求a+b的值;