在社会实践中,小明观察一棵桃树。他在点A处发现桃树顶端点C的仰角大小为 ,往正前方走4米后,在点B处发现桃树顶端点C的仰角大小为
,往正前方走4米后,在点B处发现桃树顶端点C的仰角大小为 .
.
(I) 求BC的 长;
长;
(II) 若小明身高为1.70米,求这棵桃树顶端点C离地面的高度(精确到0.01米,其中 ).
).
已知数列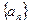 的前
的前 项和
项和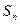 满足
满足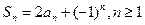 .求数列
.求数列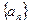 的通项公式。
的通项公式。
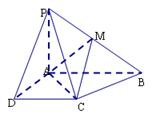
已知如图,四棱锥P-ABCD的底面为直角梯形,AB∥DC, 底面ABCD,且PA=AD=DC=
底面ABCD,且PA=AD=DC=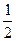 AB=1,M是PB的中点
AB=1,M是PB的中点
(Ⅰ)证明:面PAD⊥面PCD;
(Ⅱ)求AC与PB所成的角;
(Ⅲ)求面AMC与面BMC所成二面角的大小
等差数列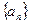 是递增数列,前n项和为
是递增数列,前n项和为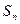 ,且
,且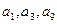 成等比数列,
成等比数列,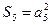 .求数列
.求数列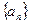 的通项公式.
的通项公式.
如图,在长方体ABCD-A1B1C1D1中,已知AB=AA1=a,BC= a,M是AD的中点。
a,M是AD的中点。
(Ⅰ)求证:AD∥平面A1BC;
(Ⅱ)求证:平面A1MC⊥平面A1BD1;
(Ⅲ)求点A到平面A1MC的距离。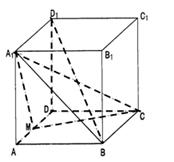
(本题满分13分)已知数列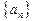 中
中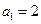 ,点
,点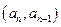 在函数
在函数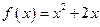 的图
的图 像上
像上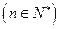 ,(1)求
,(1)求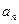 ,(2)若
,(2)若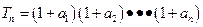 ,求
,求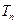 .
.