如图,在长方体ABCD-A1B1C1D1中,已知AB=AA1=a,BC= a,M是AD的中点。
a,M是AD的中点。
(Ⅰ)求证:AD∥平面A1BC;
(Ⅱ)求证:平面A1MC⊥平面A1BD1;
(Ⅲ)求点A到平面A1MC的距离。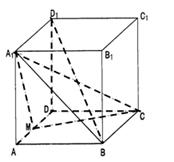
(本小题满分12分)已知 有两个不等的负根,
有两个不等的负根, 无实根,若p、q一真一假,求m的取值范围。
无实根,若p、q一真一假,求m的取值范围。
(本小题满分10分)已知圆 与直线
与直线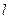 交于
交于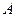 、
、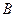 两点,若线段
两点,若线段 的中点
的中点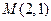
(1)求直线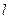 的方程;
的方程;
(2)求弦 的长.
的长.
设函数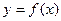
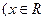 且
且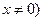 对任意非零实数
对任意非零实数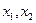 恒有
恒有 ,且对任意
,且对任意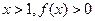 .
.
(Ⅰ)求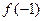 及
及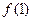 的值;
的值;
(Ⅱ)判断函数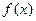 的奇偶性;
的奇偶性;
(Ⅲ)求方程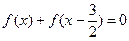 的解.
的解.
已知函数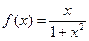 .
.
(Ⅰ)判断函数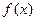 的奇偶性;
的奇偶性;
(Ⅱ)指出该函数在区间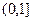 上的单调性,并用单调性定义证明;
上的单调性,并用单调性定义证明;
(Ⅲ)对于任意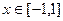 ,
,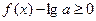 恒成立,求实数
恒成立,求实数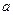 的取值范围.
的取值范围.
2005年10月12日,我国成功发射了“神州”六号载人飞船,这标志着中国人民又迈出了具有历史意义的一步.已知火箭的起飞重量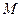 是箭体(包括搭载的飞行器)的重量
是箭体(包括搭载的飞行器)的重量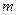 和燃料重量
和燃料重量 之和.在不考虑空气阻力的条件下,假设火箭的最大速度
之和.在不考虑空气阻力的条件下,假设火箭的最大速度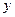 关于
关于 的函数关系式为:
的函数关系式为: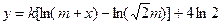 (其中
(其中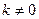 );当燃料重量为
);当燃料重量为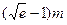 吨(
吨(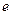 为自然对数的底数,
为自然对数的底数,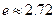 )时,该火箭的最大速度为
)时,该火箭的最大速度为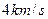 .
.
(Ⅰ)求火箭的最大速度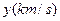 与燃料重量
与燃料重量 吨之间的函数关系式
吨之间的函数关系式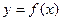 ;(要求简化表达式)
;(要求简化表达式)
(Ⅱ)已知该火箭的起飞重量是544吨,则应装载多少吨燃料,才能使该火箭的最大飞行速度达到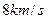 ,顺利地把飞船发送到预定的轨道?
,顺利地把飞船发送到预定的轨道?