设项数均为 (
(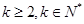 )的数列
)的数列 、
、 、
、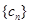 前
前 项的和分别为
项的和分别为 、
、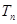 、
、 .已知
.已知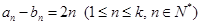 ,且集合
,且集合 =
=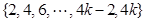 .
.
(1)已知 ,求数列
,求数列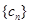 的通项公式;
的通项公式;
(2)若 ,求
,求 和
和 的值,并写出两对符合题意的数列
的值,并写出两对符合题意的数列 、
、 ;
;
(3)对于固定的 ,求证:符合条件的数列对(
,求证:符合条件的数列对( ,
, )有偶数对.
)有偶数对.
(本小题满分10分,矩阵与变换)已知矩阵 ,
, ,若矩阵
,若矩阵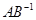 对应的变换把直线
对应的变换把直线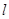 变为直线
变为直线 ,求直线
,求直线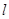 的方程.
的方程.
【原创】选修4-1:几何证明选讲(本小题满分10分)
如图,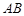 ,
,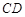 是圆
是圆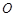 的两条弦,它们相交于
的两条弦,它们相交于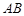 的中点
的中点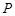 ,若
,若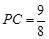 ,
,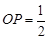 ,
,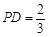 ,求圆
,求圆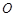 的半径.
的半径.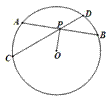
设数列 是各项均为正数的等比数列,其前
是各项均为正数的等比数列,其前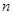 项和为
项和为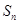 ,若
,若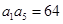 ,
,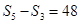 .
.
(1)求数列 的通项公式;
的通项公式;
(2)对于正整数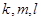 (
(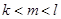 ),求证:“
),求证:“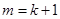 且
且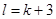 ”是“
”是“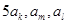 这三项经适当排序后能构成等差数列”成立的充要条件;
这三项经适当排序后能构成等差数列”成立的充要条件;
(3)设数列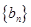 满足:对任意的正整数
满足:对任意的正整数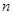 ,都有
,都有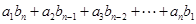
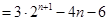 ,且集合
,且集合 中有且仅有3个元素,试求
中有且仅有3个元素,试求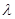 的取值范围.
的取值范围.
(本小题满分16分)已知函数 ,实数
,实数 满足
满足 ,设
,设 .
.
(1)当函数 的定义域为
的定义域为 时,求
时,求 的值域;
的值域;
(2)求函数关系式 ,并求函数
,并求函数 的定义域;
的定义域;
(3)求 的取值范围.
的取值范围.
【原创】在平面直角坐标系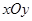 中,椭圆
中,椭圆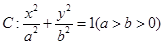 的左顶点为
的左顶点为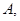 左焦点为
左焦点为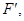 右焦点为
右焦点为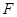 .
.
(1)若椭圆上存在点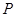 ,使得
,使得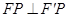 ,求椭圆
,求椭圆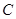 离心率的取值范围;
离心率的取值范围;
(2)若点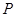 满足
满足 ,求证:以
,求证:以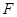 为圆心,以
为圆心,以 为半径的圆与椭圆
为半径的圆与椭圆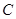 右准线相切.
右准线相切.