设数列 是各项均为正数的等比数列,其前
是各项均为正数的等比数列,其前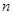 项和为
项和为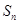 ,若
,若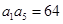 ,
,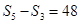 .
.
(1)求数列 的通项公式;
的通项公式;
(2)对于正整数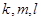 (
(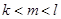 ),求证:“
),求证:“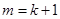 且
且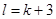 ”是“
”是“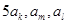 这三项经适当排序后能构成等差数列”成立的充要条件;
这三项经适当排序后能构成等差数列”成立的充要条件;
(3)设数列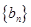 满足:对任意的正整数
满足:对任意的正整数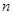 ,都有
,都有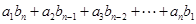
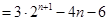 ,且集合
,且集合 中有且仅有3个元素,试求
中有且仅有3个元素,试求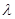 的取值范围.
的取值范围.
已知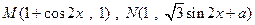
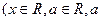 是常数),且
是常数),且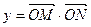 (
( 为坐标原点).
为坐标原点).
(1)求函数 的单调递增区间;
的单调递增区间;
(2)若 时,
时, 的最大值为4,求
的最大值为4,求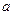 的值;
的值;
已知 是椭圆
是椭圆 的左、右焦点,过点
的左、右焦点,过点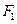 作
作
倾斜角为 的直线
的直线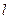 交椭圆于
交椭圆于 两点,
两点, .
.
(1)求椭圆的离心率;
(2)若 ,求椭圆的标准方程.
,求椭圆的标准方程.
已知函数 的图象经过点
的图象经过点 ,曲线在点
,曲线在点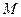 处的切线恰好与
处的切线恰好与
直线 垂直.
垂直.
(1)求实数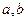 的值;
的值;
(2)若函数 在区间
在区间 上单调递增,求
上单调递增,求 的取值范围.
的取值范围.
已知函数 .
.
(1)解关于 的不等式
的不等式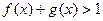 ;
;
(2)若对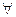
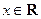 ,
, 恒成立,求
恒成立,求 的取值范围.
的取值范围.
已知直线 的参数方程为
的参数方程为 (t为参数),曲线C的极坐标方程是
(t为参数),曲线C的极坐标方程是 以极点为原点,极轴为x轴正方向建立直角坐标系,点
以极点为原点,极轴为x轴正方向建立直角坐标系,点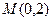 ,直线
,直线 与曲
与曲
线C交于A,B两点.
(1)写出直线 的普通方程与曲线C的直角坐标方程;
的普通方程与曲线C的直角坐标方程;
(2)线段MA,MB长度分别记|MA|,|MB|,求|MA|·|MB|的值.