( (本题满分12分)
在一次抗洪抢险中,准备用射击的方法引爆从桥上游漂流而下的一巨大汽油罐.已知
只有5发子弹备用,且首次命中只能使汽油流出,再次命中才能引爆成功,每次射击命中率都是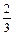 .,每次命中与否互相独立.
.,每次命中与否互相独立.
(1)求油罐被引爆的概率。
(2)如果引爆或子弹打光则停止射击,设射击次数为ξ,求ξ的分布列及ξ的数学期望。
设函数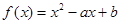 .
.
(Ⅰ)讨论函数 在
在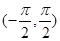 内的单调性并判断有无极值,有极值时求出极值;
内的单调性并判断有无极值,有极值时求出极值;
(Ⅱ)记 ,求函数
,求函数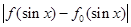 在
在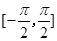 上的最大值D;
上的最大值D;
(Ⅲ)在(Ⅱ)中,取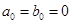 ,求
,求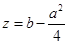 满足
满足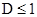 时的最大值.
时的最大值.
设函数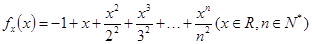 ,证明:
,证明:
(Ⅰ)对每个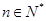 ,存在唯一的
,存在唯一的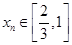 ,满足
,满足 ;
;
(Ⅱ)对任意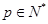 ,由(Ⅰ)中
,由(Ⅰ)中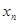 构成的数列
构成的数列 满足
满足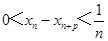 .
.
如图,已知两条抛物线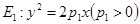 和
和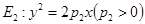 ,过原点
,过原点 的两条直线
的两条直线 和
和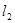 ,
, 与
与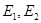 分别交于
分别交于 两点,
两点,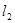 与
与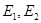 分别交于
分别交于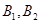 两点.
两点.
(1)证明: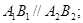
(2)过原点 作直线
作直线 (异于
(异于 ,
,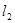 )与
)与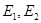 分别交于
分别交于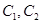 两点.记
两点.记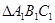 与
与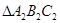 的面积分别为
的面积分别为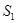 与
与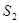 ,求
,求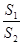 的值.
的值.
如图所示,在多面体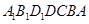 ,四边形
,四边形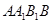 ,
, 均为正方形,
均为正方形,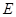 为
为 的中点,过
的中点,过 的平面交
的平面交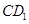 于F.
于F.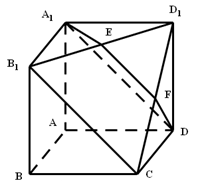
(Ⅰ)证明: ;
;
(Ⅱ)求二面角 余弦值.
余弦值.
甲乙两人进行围棋比赛,约定先连胜两局者直接赢得比赛,若赛完5局仍未出现连胜,则判定获胜局数多者赢得比赛,假设每局甲获胜的概率为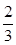 ,乙获胜的概率为
,乙获胜的概率为 ,各局比赛结果相互独立.
,各局比赛结果相互独立.
(1)求甲在4局以内(含4局)赢得比赛的概率;
(2)记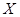 为比赛决出胜负时的总局数,求
为比赛决出胜负时的总局数,求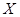 的分布列和均值(数学期望).
的分布列和均值(数学期望).