(本小题满分12分)某校高二年级有500名学生,为了了解数学学科的学习情况,现从中随机抽出若干名学生在一次测试中的数学成绩,制成如下频率分布表:
| 分组 |
频数 |
频率 |
| [85,95) |
① |
② |
| [95,105) |
|
0.050 |
| [105,115) |
|
0.200 |
| [115,125) |
12 |
0.300 |
| [125,135) |
|
0.275 |
| [135,145) |
4 |
③ |
| [145,155) |
|
0.050 |
| 合计 |
|
④ |
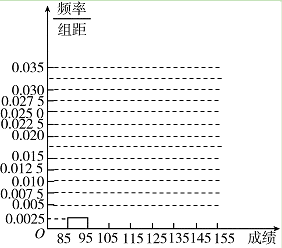
(1)根据上面图表,①②③④处的数值分别为________、________、________、________;
(2)在所给的坐标系中画出[85,155]的频率分布直方图;
(3)根据题中信息估计总体平均数,并估计总体落在[129,155]中的频率.
.已知A、B、C的坐标分别为A(4,0),B(0,4),C(3cosα,3sinα).(Ⅰ)若α∈(-π,0),且||=||,求角α的大小;(Ⅱ)若⊥,求的值.
在△ABC中,A、B、C所对边的长分别为a、b、c,已知向量=(1,2sinA),=(sinA,1+cosA),满足∥,b+c=a.(Ⅰ)求A的大小;(Ⅱ)求sin(B+)的值.
已知向量=(sinA,cosA),=(,-1),·=1,且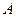 为锐角.(Ⅰ)求角A的大小;(Ⅱ)求函数f(x)=cos2x+4cosAsinx(x∈R)的值域.
为锐角.(Ⅰ)求角A的大小;(Ⅱ)求函数f(x)=cos2x+4cosAsinx(x∈R)的值域.
已知=(sinθ,),=(1,),其中θ∈(π,),则一定有()
| A.∥ | B.⊥ | C.与夹角为45° | D.||=|| |
如图,是某市1000户居民月平均用电量的频率分布直方图,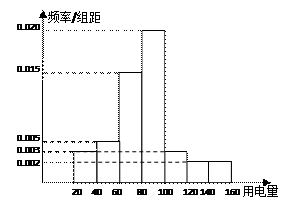
(1)如果当地政府希望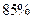 以上的居民每月的用电量不超出标准,这个标准为多少时比较适当?
以上的居民每月的用电量不超出标准,这个标准为多少时比较适当?
(2)计算这1000户居民月用电量的平均值(同一组中的数据用该组区间的中点值作代表);
(3)有关部门为了制定居民月用电量标准,采用分层抽样的方法从1000户居民中抽取50户参加听证会,并且要在这已经确定的50人中随机确定两人做中心发言,求这两人分别来自用电量区间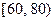 和
和 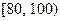 的概率.
的概率.