本小题满分12分）
在一次人才招聘会上，有A、B两家公司分别开出它们的工资标准：A公司允诺第一年月工资数为1500元，以后每年月工资比上一年月工资增加230元；B公司允诺第一年月工资数为2000元，以后每年月工资在上一年的月工资基础上递增5%，设某人年初被A、B两家公司同时录用，试问：
（1）若该人分别在A公司或B公司连续工作n年，则他在第n年的月工资收入分别是多少？
（2）该人打算连续在一家公司工作10年，仅从工资收入总量较多作为应聘的标准（其他因素不计），该人应该选择哪家公司？为什么？（参考值：
、
、
）
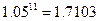某校从高一年级期末考试的学生中抽出
名学生，其成绩（均为整数）的频率分布直方图如图所示：
（Ⅰ）估计这次考试的及格率（分及以上为及格）；
（Ⅱ）估计这次考试的平均分.
.
（本小题12分）
已知函数
，（
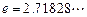）其定义域为
（
）,设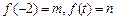
.
（1）试确定
的取值范围,使得函数
在上为单调函数；
（2）试判断
的大小并说明理由.
（本小题12分）
如图所示，将一矩形花坛ABCD扩建成一个更大的矩形花坛AMPN，要求M在AB的延长线上，N在AD的延长线上，且对角线MN过C点。已知AB=3米，AD=2米
。设
（单位：米），若
（单位：米），则当AM，AN的长度分别是多少时，花坛AMPN的面积最大？并求出最大面积。
设函数
（a、b、c、d∈R）满足：对于任意的
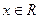都有f（x）+f（-x）=0，且x=1时f(x)取极小值
.
(1)f(x)的解析式；
(2)当
时，证明：函数图象上
任意两点处的切线不可能互相垂直：