（本小
题满分12分）
上海世
博会深圳馆1号作品《大芬丽莎》是由大芬村507名画师集体创作的999幅
油画组合而成的世界名画《蒙娜丽莎》，因其诞生于大芬村，因此被命名为《大芬丽莎》．某部门从参加创作的507名画师中随机抽出100名画师，测得画师年龄情况如下表所示．
| 分 组 （单位：岁） |
频数 |
频 率 |
 |
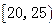5 |
0．050 |
 |
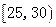① |
0．200 |
 |
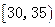35 |
② |
 |
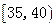30 |
0．300 |
 |
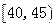10 |
0．100 |
| 合 计 |
100 |
1．00 |
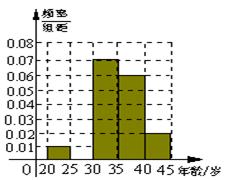
（1）频率分布表中的①、②位置应填什么数据？并在答题卡中补全频率分布直方图，
再根据频率分布直方图估计这507名画师中年龄
在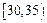
岁的人数（结果取整数）；
（2）在抽出的100名画师中按年龄再采用分层抽样法抽取20人参加上海世博会
深
圳馆志愿者活动，其中选取2名
画师担任解说员工作，记这2名画师中“年龄低于30岁”的人数为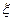
，求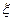的分布列及数学期望．
已知一个圆锥的母线长为20cm，当圆锥的高为多少时体积最大？最大体积是多少？
(1)已知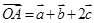
，
，
，
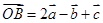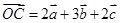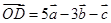，其中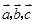
三向量不共面．试判断A，B，C，D四点是否共面？
(2)设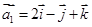
，
，
，
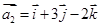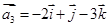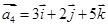．试问是否存在实数
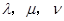，使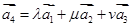
成立？如果存在，求出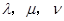；如果不存在，请给出理由．
企业管理者通过对某电子产品制造厂做上午班工人工作效率的研究表明，一个中等技术水平的工人，从8:00开始工作，t小时后可装配某电子产品的个数为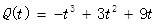
，则这个工人从8:00到12:00何时的工作效率最高？
已知椭圆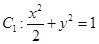
.
（1）我们知道圆具有性质：若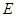
为圆O：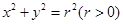
的弦AB的中点，则直线AB的斜率
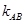与直线OE的斜率
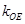的乘积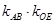
为定值。类比圆的这个性质，写出椭圆
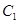的类似性质，并加以证明；
（2）如图（1），点B为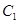在第一象限中的任意一点，过B作
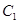的切线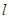
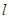，分别与x轴和y轴的正半轴交于C，D两点，求三角形OCD面积的最小值；
（3）如图（2），过椭圆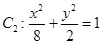
上任意一点
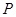作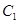的两条切线PM和PN，切点分别为M，N.当点P在椭圆
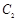上运动时，是否存在定圆恒与直线MN相切？若存在，求出圆的方程；若不存在，请说明理由.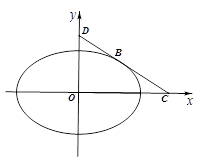
图（1）图（2）
设函数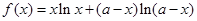
．
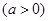（1）当
时，求函数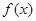
的最小值；
（2）证明：对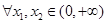
，都有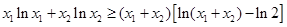
；