(本小题满分14分)
设函数 ,方程
,方程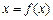 有唯一解,其中实数
有唯一解,其中实数 为常数,
为常数, ,
,
(1)求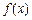 的表达式;
的表达式;
(2)求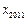 的值;
的值;
(3)若 且
且 ,求证:
,求证: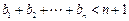
(本小题满分12分)
设 和
和 .
.
已知函数 .(Ⅰ)求不等式
.(Ⅰ)求不等式 的解集;
的解集;
(Ⅱ)若关于 的不等式
的不等式 的解集非空,求实数
的解集非空,求实数 的取值范围.
的取值范围.
如图,在正△ABC中,点D,E分别在边AC, AB上,且AD=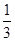 AC, AE=
AC, AE=  AB,BD,CE相交于点F。
AB,BD,CE相交于点F。
(I)求证:A,E,F,D四点共圆;
(Ⅱ)若正△ABC的边长为2,求,A,E,F,D所在圆的半径.
(本小题满分12分)设 和
和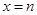 是函数
是函数 的两个极
的两个极
值点,其中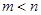 ,
, .(Ⅰ) 求
.(Ⅰ) 求 的取值范围;
的取值范围;
(Ⅱ) 若 ,求
,求 的最大值.
的最大值.
(本小题满分12分)如图,在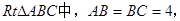 点
点 上,过点
上,过点 做
做 //
// 将
将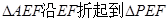 的位置(
的位置( ),
),
使得 .
.
(I)求证: (II)试问:当点
(II)试问:当点 上移动时,二面角
上移动时,二面角 的平面角的余弦值是否为定值?若是,求出定值,若不是,说明理由.
的平面角的余弦值是否为定值?若是,求出定值,若不是,说明理由.