高三第一学期期末四校联考数学第I卷中共有8道选择题,每道选择题有4个选项,其中只有一个是正确的;评分标准规定:“每题只选一项,答对得5分,不答或答错得0分。”某考生每道题都给出一个答案,已确定有5道题的答案是正 确的,而其余选择题中,有1道题可判断出两个选项是错误的,有一道可以判断出一个选项是错误的,还有一道因不了解题意只能乱猜,试求出该考生:
确的,而其余选择题中,有1道题可判断出两个选项是错误的,有一道可以判断出一个选项是错误的,还有一道因不了解题意只能乱猜,试求出该考生:
(1)得40分的概率
(2)得多少分的可能性最大?
(3)所得分数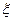 的数学期望
的数学期望
已知 是全不相等的正实数,证明:
是全不相等的正实数,证明: .
.
如图,抛物线 与
与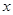 轴交于两点
轴交于两点 ,点
,点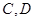 在抛物线上(点
在抛物线上(点 在第一象限),
在第一象限), ∥
∥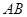 .记
.记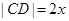 ,梯形
,梯形 面积为
面积为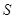 .
.
(1)求面积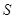 以
以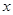 为自变量的函数式;
为自变量的函数式;
(2)若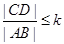 ,其中
,其中 为常数,且
为常数,且 ,求
,求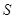 的最大值.
的最大值.
已知椭圆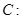
 的离心率为
的离心率为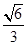 ,一个焦点为
,一个焦点为 .
.
(Ⅰ)求椭圆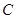 的方程;
的方程;
(Ⅱ)设直线 交椭圆
交椭圆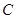 于
于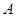 ,
, 两点,若点
两点,若点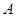 ,
, 都在以点
都在以点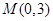 为圆心的圆上,求
为圆心的圆上,求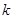 的值.
的值.
某少数民族的刺绣有着悠久的历史,如右图(1)、(2)、(3)、(4)为她们刺绣最简单的四个图案,这些图案都是由小正方形构成,小正方形数越多刺绣越漂亮.现按同样的规律刺绣(小正方形的摆放规律相同),设第n个图形包含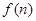 个小正方形.
个小正方形.
(1)求出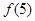 的值;
的值;
(2)利用合情推理的“归纳推理思想”,归纳出 与
与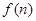 之间的关系式,并根据你得到的关系式求出
之间的关系式,并根据你得到的关系式求出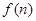 的表达式;
的表达式;
(3)求 的值。
的值。
已知双曲线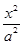 -
- =1(a>0,b>0)的离心率e=
=1(a>0,b>0)的离心率e=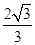 ,直线l过A(a,0),B(0,-b)两点,原点O到直线l的距离是
,直线l过A(a,0),B(0,-b)两点,原点O到直线l的距离是 .
.
(1)求双曲线的方程;
(2)过点B作直线m交双曲线于M、N两点,若 ·
· =-23,求直线m的方程.
=-23,求直线m的方程.