.(本小题满分12分)
已知椭圆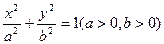
 与双曲线
与双曲线 有共同的焦点F1、F2,设它们在第一象限的交点为P,且
有共同的焦点F1、F2,设它们在第一象限的交点为P,且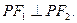
(1)求椭圆的方程;
(2)已知N(0,-1),对于(1)中的椭圆,是否存在斜率为 的直线
的直线 ,与椭圆交于不同的两点A、B,点Q满足
,与椭圆交于不同的两点A、B,点Q满足 ?若存在,求出
?若存在,求出 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
.(13分)已知三次函数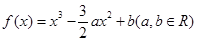 .
.
(1)若曲线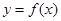 在点
在点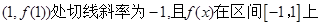 最大值
最大值 求函数
求函数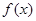 的解析式.
的解析式.
(2)若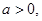 解关于x的不等式
解关于x的不等式
(13分)已知钝角三角形 中,
中,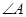 为钝角,若向量
为钝角,若向量 .且
.且 . (1)求
. (1)求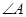 的大小; (2)设函数
的大小; (2)设函数 ,若
,若 恒成立,求实数
恒成立,求实数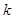 的取值范围.
的取值范围.
(本小题满分12分)
已知以原点为中心,F( ,0)为右焦点的椭圆C,过点F垂直于
,0)为右焦点的椭圆C,过点F垂直于 轴的弦AB长为4.
轴的弦AB长为4.
(1).求椭圆C的标准方程.
(2).设M、N为椭圆C上的两动点,且 ,点P为椭圆C的右准线与
,点P为椭圆C的右准线与 轴的交点,求
轴的交点,求 的取值
的取值 范围.
范围.
(本小题满分12分)
如图所示,正四棱锥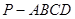 中,AB=1,侧棱
中,AB=1,侧棱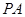 与底面
与底面 所成角的正切值为
所成角的正切值为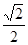 .
.
(1)求二面角P-CD-A的大小.
(2)设点F在AD上,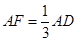 ,求点A到平面PB
,求点A到平面PB F的距离.
F的距离.

(本小题满分12分)
已知函数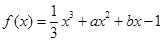 的导函数
的导函数 为偶函数,直线
为偶函数,直线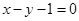 是
是 的一条切线.(1).求
的一条切线.(1).求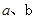 的值 (2).若
的值 (2).若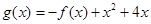 ,求
,求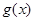 的极值.
的极值.