某中学高三文科班学生参加了数学与地理水平测试,学校从测试合格的学生中随机抽取100人的成绩进行统计分析.抽取的100人的数学与地理的水平测试成绩如下表: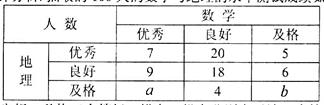
成绩分为优秀、良好、及格三个等级,横向、纵向分别表示地理成绩与数学成绩,例如:表中数学成绩为良好的共有20+18+4=42人.
(1)若在该样本中,数学成绩优秀率为30%,求a,b的值;
(2)若样本中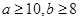 ,求在地理成绩及格的学生中,数学成绩优秀的人数比及格的人数少的概率.
,求在地理成绩及格的学生中,数学成绩优秀的人数比及格的人数少的概率.
已知函数 的部分图象如图所示.
的部分图象如图所示.
(1)求函数 的解析式,并写出
的解析式,并写出 的单调减区间;
的单调减区间;
(2)已知 的内角分别是A,B,C,角A为锐角,且
的内角分别是A,B,C,角A为锐角,且 的值.
的值.
“光盘行动”倡导厉行节约,反对铺张浪费,带动大家珍惜粮食,吃光盘子中的食物,得到从中央到民众的支持,为了解某地响应“光盘行动”的实际情况,某校几位同学组成研究性学习小组,从某社区 岁的人群中随机抽取n人进行了一次调查,得到如下统计表:
岁的人群中随机抽取n人进行了一次调查,得到如下统计表:
(1)求a,b的值,并估计本社区 岁的人群中“光盘族”所占比例;
岁的人群中“光盘族”所占比例;
(2)从年龄段在 的“光盘族”中,采用分层抽样方法抽取8人参加节约粮食宣传活动,并从这8人中选取2人作为领队.
的“光盘族”中,采用分层抽样方法抽取8人参加节约粮食宣传活动,并从这8人中选取2人作为领队.
(1)已知选取2人中1人来自 中的前提下,求另一人来自年龄段
中的前提下,求另一人来自年龄段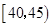 中的概率;
中的概率;
(2)求2名领队的年龄之和的期望值(每个年龄段以中间值计算).
如图,在梯形ABCD中,AB//CD,AD=DC=CB=a,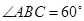 ,平面
,平面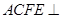 平面ABCD,四边形ACFE是矩形,AE=a.
平面ABCD,四边形ACFE是矩形,AE=a.
(1)求证: 平面ACFE;
平面ACFE;
(2)求二面角B—EF—D的平面角的余弦值.
已知等差数列 的首项
的首项 ,公差
,公差 ,等比数列
,等比数列 满足
满足
(1)求数列 和
和 的通项公式;
的通项公式;
(2)设数列 对任意
对任意 均有
均有 ,求数列
,求数列 的前n项和
的前n项和 .
.