(本题9分)
已知等差数列﹛an﹜满足:a3=1 5, a5+a7=18。
5, a5+a7=18。
(1)求数列﹛an﹜的通项an;
(2)设﹛bn-an﹜是首项为1,公比为3的等比数列,求数列﹛bn﹜的通项公式和前n项和Sn。
(本小题满分13分)已知函数 .
.
(1)求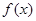 的单调区间;
的单调区间;
(2)已知数列 的通项公式为
的通项公式为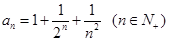 ,求证:
,求证: (
( 为自然对数的底数);
为自然对数的底数);
(3)若 ,且
,且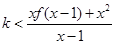 对任意
对任意 恒成立,求
恒成立,求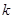 的最大值。
的最大值。
(本小题满分13分)如图,某工厂生产的一种无盖纸筒为圆锥形,现一客户订制该圆锥纸筒,并要求该圆锥纸筒的容积为π立方分米.设圆锥纸筒底面半径为r分米,高为h分米.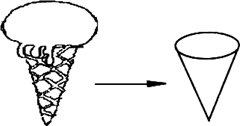
(1)求出r与h满足的关系式;
(2)工厂要求制作该纸筒的材料最省,求最省时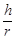 的值.
的值.
(本小题满分13分)已知等差数列 的公差为
的公差为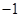 ,首项为正数,将数列
,首项为正数,将数列 的前
的前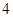 项抽去其中一项后,剩下三项按原来顺序恰为等比数列
项抽去其中一项后,剩下三项按原来顺序恰为等比数列 的前3项,
的前3项,
(1)求数列 的通项公式
的通项公式 与前
与前 项和
项和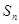 ;
;
(2)是否存在三个不等正整数 ,使
,使 成等差数列且
成等差数列且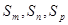 成等比数列.
成等比数列.
(本小题满分12分)在多面体 中,
中,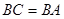 ,
,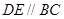 ,
,  平面
平面 ,
,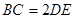 ,
, 为
为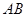 的中点.
的中点.
(1)求证: 平面
平面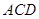 ;
;
(2)若 ,求二面角
,求二面角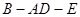 的正切值的大小.
的正切值的大小.
(本小题满分12分)已知数列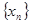 满足
满足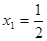 ,
,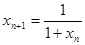 ,
,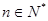 .猜想数列
.猜想数列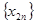 的单调性,并证明你的结论.
的单调性,并证明你的结论.