:如图,两个工厂 相距
相距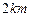 ,点
,点 为
为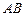 的中点,现要在以
的中点,现要在以 为圆心,
为圆心,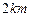 为半径的圆弧
为半径的圆弧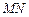 上的某一点
上的某一点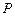 处建一幢办公楼,其中
处建一幢办公楼,其中 .据测算此办公楼受工厂
.据测算此办公楼受工厂 的“噪音影响度”与距离
的“噪音影响度”与距离 的平方成反比,比例系数是1,办公楼受工厂
的平方成反比,比例系数是1,办公楼受工厂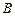 的“噪音影响度” 与距离
的“噪音影响度” 与距离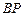 的平方也成反比,比例系数是4,办公楼受
的平方也成反比,比例系数是4,办公楼受 两厂的“总噪音影响度”
两厂的“总噪音影响度” 是受
是受 两厂“噪音影响度”的和,设
两厂“噪音影响度”的和,设 为
为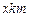 .
.
(Ⅰ)求“总噪音影响度”  关于
关于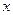 的函数关系,并求出该函数的定义域;
的函数关系,并求出该函数的定义域;
(Ⅱ)当 为多少时,“总噪音影响度”最小?
为多少时,“总噪音影响度”最小?
现测得∠BCD=53°,∠BDC=60°,CD=60(米),并在点C测得塔顶A的仰角为∠ACB=29°,求塔高AB(精确到0.1米).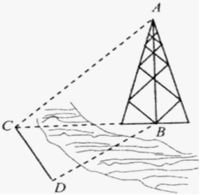
已知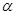 ,
, 为锐角,
为锐角,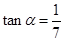 ,
,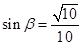 ,求
,求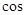 (
( ).
).
已知等差数列{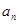 }中,
}中, =8,前10项和S10=185.
=8,前10项和S10=185.
(1)求通项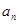 ;
;
(2)若 是由
是由 ……组成,试归纳
……组成,试归纳 的一个通项公式.
的一个通项公式.
(本小题满分16分)已知函数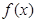 =
=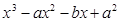 ,
,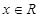 ,
,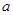 ,
,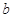 为常数。
为常数。
(1)若函数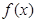 在
在 =1处有极值10,求实数
=1处有极值10,求实数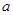 ,
,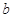 的值;
的值;
(2)若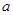 =0,(I)方程
=0,(I)方程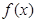 =2在
=2在 ∈[-4,4]上恰有3个不相等的实数解,求实数
∈[-4,4]上恰有3个不相等的实数解,求实数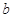 的取值范围;(II)不等式
的取值范围;(II)不等式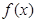 +2
+2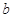 ≥0对
≥0对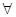
 ∈[1,4]恒成立,求实数
∈[1,4]恒成立,求实数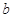 的取值范围。
的取值范围。
(本小题满分16分) 已知圆 的方程为
的方程为 ,直线
,直线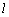 的方程为
的方程为 ,点
,点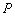 在直线
在直线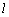 上,过
上,过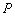 点作圆
点作圆 的切线
的切线 ,切点为
,切点为 .
.
(1)若 ,试求点
,试求点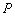 的坐标;
的坐标;
(2)若 点的坐标为
点的坐标为 ,过
,过 作直线与圆
作直线与圆 交于
交于 两点,当
两点,当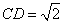 时,求直线
时,求直线 的方程
的方程
(3)经过 三点的圆是否经过异于点M的定点,若经过,请求出此定点的坐标;若不经过,请说明理由。
三点的圆是否经过异于点M的定点,若经过,请求出此定点的坐标;若不经过,请说明理由。