、 已知 ≤
≤ ≤1,若函数
≤1,若函数 在区间[1,3]上的最大值为
在区间[1,3]上的最大值为 ,最小值为
,最小值为 ,令
,令 .
.
(1)求 的函数表达式;
的函数表达式;
(2)判断并证明函数 在区间[
在区间[ ,1]上的单调性;并求出
,1]上的单调性;并求出 的最小值 .
的最小值 .
(本小题满分14分)现有一批货物用轮船从甲地运往乙地,甲乙两地距离为500海里,已知该船最大速度为45海里/小时,每小时运输成本由燃料费用和其它费用组成.轮船每小时的燃料费用与轮船速度的平方成正比,其余费用为每小时960元.已知轮船速度为20海里/小时,全程运输成本为30000元.
(1)把全程运输成本 (元)表示为速度
(元)表示为速度 (海里/小时)的函数;
(海里/小时)的函数;
(2)为了使全程运输成本最小,轮船应为多大速度行驶?
(本小题满分14分)如图,椭圆以边长为1的正方形ABCD的对角顶点A,C为焦点,且经过各边的中点,试建立适当的坐标系,求椭圆的方程。
如果双曲线的两个焦点分别为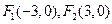 ,一条渐近线方程为:
,一条渐近线方程为: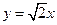
(1)求该双曲线的方程;
(2)过焦点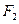 ,倾斜角为
,倾斜角为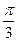 的直线与该双曲线交于
的直线与该双曲线交于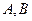 两点,求
两点,求 。
。
已知关于 的不等式
的不等式 的解集是
的解集是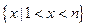 。
。
(1)求实数 的值;
的值;
(2)若正数 满足:
满足: ,求
,求 的最大值。
的最大值。
已知 ,数列
,数列 满足:
满足: 。
。
(1)用数学归纳法证明: ;
;
(2)已知 ;
;
(3)设Tn是数列{an}的前n项和,试判断Tn与n-3的大小,并说明理由。