:已知椭圆P的中心O在坐标原点,焦点在x坐标轴上,且经过点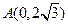 ,离心率为
,离心率为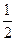
(1)求椭圆P的方程:
(2)是否存在过点E(0,-4)的直线l交椭圆P于点R,T,且满足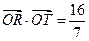 .若存在,求直线l的方程;若不存在,请说明理由.
.若存在,求直线l的方程;若不存在,请说明理由.
在四棱锥P-ABCD中,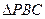 为正三角形,AB
为正三角形,AB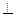 平面PBC,AB//CD,AB=
平面PBC,AB//CD,AB=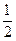 DC,E为PD中点。(1)求证:AE//平面PBC
DC,E为PD中点。(1)求证:AE//平面PBC
(2)求证:AE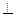 平面PDC
平面PDC
(1)f(x)="x" + 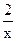 的值域为[3,9],K
的值域为[3,9],K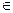 [3,9]时,f(x)=K有两不等的根x1,x2,求x1+x2.
[3,9]时,f(x)=K有两不等的根x1,x2,求x1+x2.
(2)g (x) =x+2+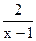 的值域为[7,11],K
的值域为[7,11],K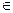 [7,11]时,g(x)=K
[7,11]时,g(x)=K
也有两不等根x3、x4,求x3+x4
(3)h(x) =x+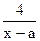 -b, x>a
-b, x>a
h(x)=K的两根之和为K+18,且h(x)的最小值为0,试求a与b的值。
函数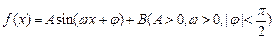 的图象上一个最高点的坐标为
的图象上一个最高点的坐标为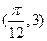 ,与之相邻的一个最低点的坐标为
,与之相邻的一个最低点的坐标为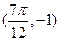 .
.
(Ⅰ)求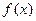 的表达式;
的表达式;
(Ⅱ)求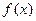 在
在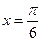 处的切线方程.
处的切线方程.
设椭圆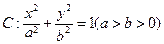 的一个顶点与抛物线
的一个顶点与抛物线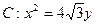 的焦点重合,
的焦点重合,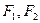 分别是椭圆的左、右焦点,且离心率
分别是椭圆的左、右焦点,且离心率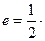 且过椭圆右焦点
且过椭圆右焦点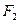 的直线
的直线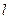 与椭圆C交于
与椭圆C交于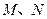 两点.
两点.
(1)求椭圆C的方程;
(2)是否存在直线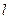 ,使得
,使得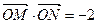 .若存在,求出直线
.若存在,求出直线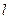 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
(3)若AB是椭圆C经过原点O的弦, MN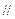 AB,求证:
AB,求证: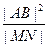 为定值.
为定值.
已知函数 (
(
 R).
R).
(1)当 时,求函数
时,求函数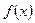 的极值;
的极值;
(2)若函数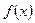 的图象与
的图象与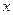 轴有且只有一个交点,求a的取值范围.
轴有且只有一个交点,求a的取值范围.