当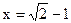 时,求代数式
时,求代数式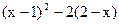 的值
的值
某公司为了提高经济效益,决定引进一条新的生产线并从现有员工中抽调一部分员工到新的生产线上工作。经调查发现:分工后,留在原生产线上工作的员工每月人均产值提高40%;到新生产线上工作的员工每月人均产值为原来的3倍。已知某公司现有员工50人,设抽调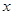 人到新生产线上工作。
人到新生产线上工作。
(1)若分工前员工每月的人均产值为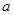 元,则分工后留在原生产线上工作的员工每月人均产值是元,每月的总产值是元;到新生产线上工作的员工每月人均产值是
元,则分工后留在原生产线上工作的员工每月人均产值是元,每月的总产值是元;到新生产线上工作的员工每月人均产值是
元,每月的总产值是元。
(2)分工后若留在原生产线上的员工每月生产的总产值不少于分工前原生产线每月生产的总产值,而且新生产线每月生产的总产值又不少于分工前生产线每月生产的总产值的一半。
问:抽调的人数应该在什么范围?
班委会决定,选购圆珠笔、钢笔共22支,送给山区学校的同学。已知圆珠笔每支5元,钢笔每支6元。
(1)若购买圆珠笔、钢笔刚好用去120元,问圆珠笔、钢笔各买了多少支?
(2)若购圆珠笔可9折优惠,钢笔可8折优惠,在所需费用不超过100元的前提下,请你写出一种选购方案。
北京举办2008年夏季奥运会以来,奥运知识在我国不断传播,小刚就本班学生对奥运知识的了解程度进行了一次调查统计。A:熟悉,B:了解较多,C:较易了解。图1和图2是他采集数据后,绘制的两幅不完整的统计图。请你根据图中提供的信息解答以下问题:
(1)求该班共有多少名学生?
(2)在条形图中,将表示“较易了解”的部分补充完整;
(3)在扇形统计图中,计算出“了解较多”部分所对应的圆心角的度数;
(4)如果全年级共1000名学生,请你估算全年级对奥运知识“了解较多”的学生人数。
2009年是执行法定节日的第一年,法定节日的确定为大家带来了很多便利。我们用坐标来表示这些节日:元旦用 表示(即1月1日),清明节用
表示(即1月1日),清明节用 表示(即4月4日),端午节用
表示(即4月4日),端午节用 表示(即5月初5)。
表示(即5月初5)。
(1)用坐标表示出中秋节 (),国庆节
(),国庆节 ();
();
(2)依次连接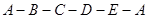 ,在给出的坐标系中画出来;
,在给出的坐标系中画出来;
(3)求所画图形的面积。
如图, 中,
中, 是高,
是高,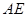 ,
,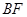 分别是
分别是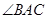 和
和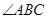 的平分线,它们相交于点
的平分线,它们相交于点 ,
, ,
,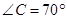 。求
。求 ,
, 。
。