北京举办2008年夏季奥运会以来,奥运知识在我国不断传播,小刚就本班学生对奥运知识的了解程度进行了一次调查统计。A:熟悉,B:了解较多,C:较易了解。图1和图2是他采集数据后,绘制的两幅不完整的统计图。请你根据图中提供的信息解答以下问题:
(1)求该班共有多少名学生?
(2)在条形图中,将表示“较易了解”的部分补充完整;
(3)在扇形统计图中,计算出“了解较多”部分所对应的圆心角的度数;
(4)如果全年级共1000名学生,请你估算全年级对奥运知识“了解较多”的学生人数。
如图1所示,已知抛物线 的顶点为D,与x轴交于A、B两点,与y轴交于C点,E为对称轴上的一点,连接CE,将线段CE绕点E按逆时针方向旋转90°后,点C的对应点C′恰好落在y轴上.
的顶点为D,与x轴交于A、B两点,与y轴交于C点,E为对称轴上的一点,连接CE,将线段CE绕点E按逆时针方向旋转90°后,点C的对应点C′恰好落在y轴上.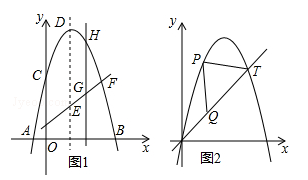
(1)直接写出D点和E点的坐标;
(2)点F为直线C′E与已知抛物线的一个交点,点H是抛物线上C与F之间的一个动点,若过点H作直线HG与y轴平行,且与直线C′E交于点G,设点H的横坐标为m(0<m<4),那么当m为何值时,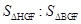 =5:6?
=5:6?
(3)图2所示的抛物线是由 向右平移1个单位后得到的,点T(5,y)在抛物线上,点P是抛物线上O与T之间的任意一点,在线段OT上是否存在一点Q,使△PQT是等腰直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
向右平移1个单位后得到的,点T(5,y)在抛物线上,点P是抛物线上O与T之间的任意一点,在线段OT上是否存在一点Q,使△PQT是等腰直角三角形?若存在,求出点Q的坐标;若不存在,请说明理由.
如图,AB、CD为⊙O的直径,弦AE∥CD,连接BE交CD于点F,过点E作直线EP与CD的延长线交于点P,使∠PED=∠C.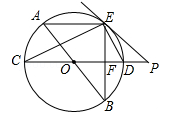
(1)求证:PE是⊙O的切线;
(2)求证:ED平分∠BEP;
(3)若⊙O的半径为5,CF=2EF,求PD的长.
如图,A为某旅游景区的最佳观景点,游客可从B处乘坐缆车先到达小观景平台DE观景,然后再由E处继续乘坐缆车到达A处,返程时从A处乘坐升降电梯直接到达C处,已知:AC⊥BC于C,DE∥BC,BC=110米,DE=9米,BD=60米,α=32°,β=68°,求AC的高度.(参考数据:sin32°≈0.53;cos32°≈0.85;tan32°≈0.62;sin68°≈0.93;cos68°≈0.37;tan68°≈2.48)
某市居民用电的电价实行阶梯收费,收费标准如下表: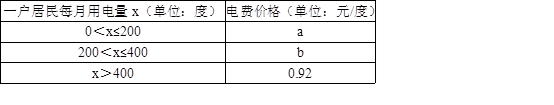
(1)已知李叔家四月份用电286度,缴纳电费178.76元;五月份用电316度,缴纳电费198.56元,请你根据以上数据,求出表格中a,b的值.
(2)六月份是用电高峰期,李叔计划六月份电费支出不超过300元,那么李叔家六月份最多可用电多少度?
如图,已知BD平分∠ABF,且交AE于点D,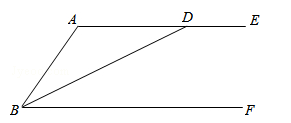
(1)求作:∠BAE的平分线AP(要求:尺规作图,保留作图痕迹,不写作法);
(2)设AP交BD于点O,交BF于点C,连接CD,当AC⊥BD时,求证:四边形ABCD是菱形.