已知直线l经过抛物线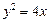 的焦点F,
的焦点F,
且与抛物线相交于A、B两点.
(1)若 ,求点A的坐标;
,求点A的坐标;
(2)若直线l的倾斜角为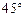 ,求线段AB的长.
,求线段AB的长.
(本小题满分14分)
已知定义在R上的单调函数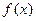 ,存在实数
,存在实数 ,使得对于任意实数
,使得对于任意实数 总有
总有 恒成立.(Ⅰ)求
恒成立.(Ⅰ)求 的值;(Ⅱ)若
的值;(Ⅱ)若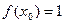 ,且对任意正整数
,且对任意正整数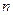 ,有
,有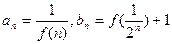 ,记
,记 ,
,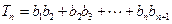 ,比较
,比较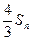 与
与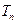 的大小关系;
的大小关系;
(Ⅲ)若不等式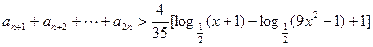 对任意不小于2的正整数
对任意不小于2的正整数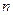 都成立,求
都成立,求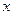 的取值范围.
的取值范围.
(本小题满分13分)
已知函数 R),设关于
R),设关于 的方程
的方程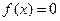 的两实根为
的两实根为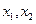 ,方程
,方程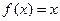 的两实根为
的两实根为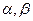 .(Ⅰ)若
.(Ⅰ)若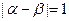 ,求
,求 的关系式;(Ⅱ)若
的关系式;(Ⅱ)若 均为负整数,且
均为负整数,且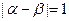 ,求
,求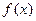 的解析式;(Ⅲ)若
的解析式;(Ⅲ)若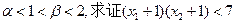 .
.
(本小题满分12分)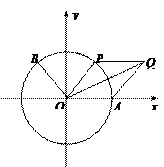 如图,
如图, 是单位圆与
是单位圆与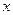 轴正半轴的交点,点
轴正半轴的交点,点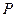 在单位圆上,
在单位圆上,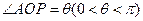 ,
, ,四边形
,四边形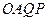 的面积为
的面积为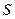 .
.
(Ⅰ)试判断四边形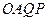 的形状并求其面积
的形状并求其面积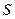 ;
;
(Ⅱ)设函数 ,求
,求
的最大值及对应的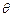 的值
的值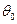 ;
;
(Ⅲ)设点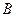 的坐标为
的坐标为 ,
,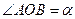 ,在(Ⅱ)的条件下,求
,在(Ⅱ)的条件下,求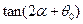 .
.
(本小题满分12分) 某建筑的金属支架如图所示,根据要求
某建筑的金属支架如图所示,根据要求 至少长
至少长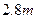 ,
,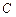 为
为 的中点,
的中点, 到
到 的距离比
的距离比 的长小
的长小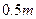 ,
,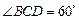 ,已知建筑支架的材料每米的价格一定,问怎样设计
,已知建筑支架的材料每米的价格一定,问怎样设计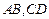 的长,可使建造这个支架的成本最低?
的长,可使建造这个支架的成本最低?
(本小题满分12分)
已知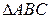 的面积为
的面积为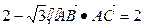 .(1)求
.(1)求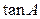 的值;
的值;
(2)求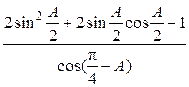 的值
的值