((本小题满分14分)
设数列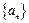 是公差为
是公差为 的等差数列,其前
的等差数列,其前 项和为
项和为 .
.
(1)已知 ,
, ,
,
(ⅰ)求当
 时,
时, 的最小值;
的最小值;
(ⅱ)当
 时,求证:
时,求证: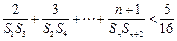 ;
;
(2)是否存在实数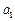 ,使得对任意正整数
,使得对任意正整数 ,关于
,关于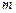 的不等式
的不等式 的最小正整数解为
的最小正整数解为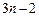 ?若存在,则求
?若存在,则求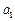 的取值范围;若不存在,则说明理由.
的取值范围;若不存在,则说明理由.
如图,底面为直角梯形的四棱锥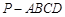 中,AD∥BC,
中,AD∥BC,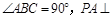 平面
平面 ,
, 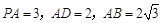 ,BC=6.
,BC=6.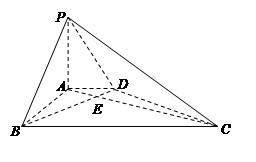
(Ⅰ)求证:BD⊥平面PAC;
(Ⅱ)求二面角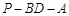 的余弦值.
的余弦值.
已知圆C: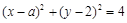 与直线l:
与直线l: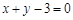 ,且直线l被圆C截得的弦长为
,且直线l被圆C截得的弦长为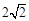 .
.
(Ⅰ)求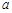 的值;
的值;
(Ⅱ)当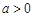 时,求过点(3,5)且与圆C相切的直线方程.
时,求过点(3,5)且与圆C相切的直线方程.
已知△ABC的两个顶点A,B的坐标分别是(-5,0),(5,0),且AC,BC所在直
线的斜率之积等于m(m≠0),求顶点C的轨迹.
已知函数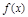 =x2-4x+a+3,g(x)=mx+5-2m.
=x2-4x+a+3,g(x)=mx+5-2m.
(Ⅰ)若方程f(x)=0在[-1,1]上有实数根,求实数a的取值范围;
(Ⅱ)当a=0时,若对任意的x1∈[1,4],总存在x2∈[1,4],使f(x1)=g(x2)成立,求实数m的取值范围;
(Ⅲ)若函数y=f(x)(x∈[t,4])的值域为区间D,是否存在常数t,使区间D的长度为7-2t?若存在,求出t的值;若不存在,请说明理由(注:区间[p,q]的长度为q-p).
已知函数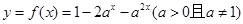
(1)求函数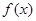 的值域;
的值域;
(2)若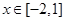 时,函数
时,函数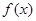 的最小值为
的最小值为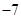 ,求
,求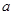 的值和函数
的值和函数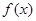 的最大值。
的最大值。